Data embedding using IBM quantum composer

Question

How do you use the IBM quantum composer to encode some data $(a,b,c,d)$ represented by a vector ket in which $a,b,c,d$ have been normalized to one? $a|00\rangle + b|01\rangle + c|10\rangle + d|11\rangle$

Answer 1

One way to do it is to use the initialize function then decomposed the circuit and print out the qasm code and pull it over to the composer...

There was a similar question to your question here

But here is an example that might help:

from qiskit import QuantumCircuit, IBMQ
import numpy as np
num_qubits = 2
vector = [1,2,3,4] #[a,b,c,d] not normalize 
initial_state = vector/np.linalg.norm(vector) #normalize the state 
circuit = QuantumCircuit(num_qubits,num_qubits)
circuit.initialize(initial_state, [0,1])  
print(circuit)
 ┌─────────────────────────────────────────────┐

q_0: ┤0                                            ├
     │  initialize(0.18257,0.36515,0.54772,0.7303) │
q_1: ┤1                                            ├
     └─────────────────────────────────────────────┘
c: 2/═══════════════════════════════════════════════

And now you can use the decomposed function to decomposed this circuit into the gates that is available within the composer:

decomposed_circuit = transpile(circuit, basis_gates=['h', 'x', 'cx', 'ccx', 't', 'tdg', 's', 'sdg', 'p' , 'rz' , 'sx' ,'sxdg','rx', 'ry','rxx' , 'rzz',] )
 ┌────────────┐┌───┐┌─────────────┐┌───┐

q_0: ┤ RY(2.0344) ├┤ X ├┤ RY(0.17985) ├┤ X ├
     ├────────────┤└─┬─┘└─────────────┘└─┬─┘
q_1: ┤ RY(2.3005) ├──■───────────────────■──
     └────────────┘

c: 2/═══════════════════════════════════════

Extracting the 'qasm' code:

print(decomposed_circuit.qasm())
print(decomposed_circuit.qasm())
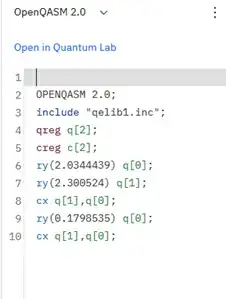
OPENQASM 2.0;
include "qelib1.inc";
qreg q[2];
creg c[2];
ry(2.0344439) q[0];
ry(2.300524) q[1];
cx q[1],q[0];
ry(0.1798535) q[0];
cx q[1],q[0];

Now take that and paste it in the QASM code block in the Circuit Composer

Now you have the initialize state that you wanted in the composer.

Answer 2

You can implement a method proposed in this article Transformation of quantum states using uniformly controlled rotations. The authors present a method for transforming any quantum state to any other one. Of course, this allow to change initial state $|0\rangle^n$ in the composer to arbitrary $n$-qubit. The method works with $CNOT$, $Ry$ and $Rz$ gates only. All these are available in the composer.

According to my knowledge, this method is implemented in Qiskit init function which proposed KAJ226 in the other answer.