Let's say I have a matrix representation, e.g.
$$ \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}. $$
How can I determine whether a quantum circuit can be constructed given said matrix representation? Is unitarity a sufficient and necessary condition?
Correct, unitarity is a sufficient and necessary condition. From Nielson and Chuang page 18:
Amazingly, this unitary constraint is the only constraint on quantum gates. Any unitary matrix specifies a valid quantum gate! The interesting implication is that in contrast to the classical case, where only one non-trivial single bit gate exists - the NOT gate - there are many non-trivial single qubit gates.
Right. But when you build a quantum computer, you want to have a certain set of gates that you want to implement, and all other gates (unitary matrices) can be built from that set of gates. This is known as a universal set. Surprisingly (or not), it is quite small. One example of a universal set is: $G = \{H, S, T, CNOT \}$ where
$$H = \dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 & 1\\ 1 & -1 \end{pmatrix}, \hspace{.25 cm} T =\begin{pmatrix} 1 & 0\\ 0 & e^{i\pi/4} \end{pmatrix}, \hspace{.25 cm} S = \begin{pmatrix} 1 & 0\\ 0 & i \end{pmatrix}, \hspace{.25 cm} CNOT = \begin{pmatrix} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} $$
This is just an example of one of many universal sets. These are the native gates you can say on your quantum hardware. For instance, on IBM hardware, the native gates are: { CNOT, I, RZ, SX, X }. The point is every unitary matrix can be approximated to an arbitrary, $\epsilon$, error using those gates. This formed your quantum circuit.
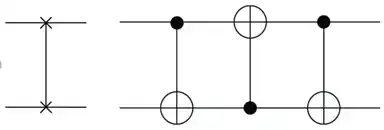
The matrix example you gave is the matrix representation of the SWAP gate. It is not a native gate on a quantum hardware but this is because you can simply implement it as a sequence of CNOT gates as follows:
