The figure of a circuit and the state are as follows.
The final state before the measurement is $|O_{out}\rangle=\frac{1}{2}|0\rangle(|\phi\rangle|\psi\rangle+|\psi\rangle|\phi\rangle)+\frac{1}{2}|1\rangle(|\phi\rangle|\psi\rangle-|\psi\rangle|\phi\rangle)$.
Measuring the first qubit of this state produces outcome 1, how can I get the probability $\frac12(1-|\langle\phi|\psi\rangle|^2)$?
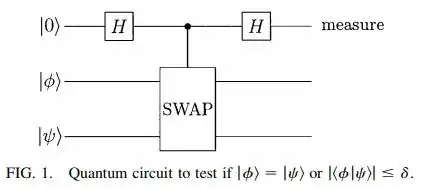
It's a fantastic question because the typical measurement intuition we apply no longer is sufficient - it's really necessary to formalize measurement.
Specifically, we create a set of nonlinear operators $M_\psi = |\psi \rangle \langle \psi |$, where the probability of measuring $\psi$ on an arbitrary state $|\phi\rangle $ is $\langle \phi | M^\dagger M | \phi \rangle$.
In our case, we have a measurement operator $M_1$ we are interested in. However, we can actually apply $M_0$ for simplicity, and then subtract this probability from 1. Thus, where $| \varphi \rangle $ is the state provided above:
\begin{align} \langle \varphi | M^\dagger M | \varphi \rangle &= \langle \varphi |0\rangle \langle 0| 0\rangle \langle 0|\varphi\rangle \\ &= \langle \varphi|0\rangle\langle 0|\varphi\rangle \\ &= \frac{1}{4} (\langle \phi|\langle \psi| + \langle \psi|\langle \phi|)( |\phi \rangle |\psi \rangle + |\psi \rangle |\phi \rangle) \\ &= \frac{1}{4}(2 \langle\phi| \langle\psi|\phi\rangle |\psi\rangle + 2) \\ &= \frac{1}{2}\Big(|\langle\psi|\phi\rangle|^2 + 1 \Big) \end{align}
Thus, because this is the zero probability, we have:
$$ 1 - \frac{1}{2}\Big(|\langle\psi|\phi\rangle|^2 + 1 \Big) = \frac{1 - |\langle \psi|\phi \rangle|^2}{2} = \frac{1 - |\langle \phi|\psi \rangle|^2}{2} $$
As desired.
I assume you're happy with the idea that the state before measurement is $$|O_{out}\rangle=\frac12|0\rangle(|\phi\rangle|\psi\rangle+|\psi\rangle|\phi\rangle)+\frac{1}{2}|1\rangle(|\phi\rangle|\psi\rangle-|\psi\rangle|\phi\rangle).$$ Now you want to measure qubit 1 in the 0/1 basis. There's a couple of different ways you might approach this.
Define the two measurement projectors to be $P_0=|0\rangle\langle 0|\otimes I\otimes I$ (i.e. measure first qubit in 0, and do nothing to the other two), and $P_1=|1\rangle\langle 1|\otimes I\otimes I$. The probability of getting the 0 answer is $\langle O_{out}|P_0|O_{out}\rangle$.
Alternative, rewrite your state as $$ |O_{out}\rangle=\gamma_0|0\rangle|\sigma\rangle+\gamma_1|1\rangle|\tau\rangle, $$ where $|\sigma\rangle$ and $|\tau\rangle$ are properly normalised vectors, and the coefficients $\gamma_{0/1}$ compensate for that normalisation. The probability of getting the answer 0 when you measure the first qubit is $|\gamma_0|^2$. So, we have $$ \gamma_0|\sigma\rangle=\frac12(|\phi\rangle|\psi\rangle+|\psi\rangle|\phi\rangle). $$ Take the inner product of that equation with itself and you get \begin{align*} |\gamma_0|^2&=\frac14(\langle\phi |\langle\psi |+\langle\psi |\langle\phi|)(|\phi\rangle|\psi\rangle+|\psi\rangle|\phi\rangle) \\ &=\frac14(2+2|\langle\phi|\psi\rangle|^2). \end{align*} The actual question requires the probability of getting answer 1. This is left as an exercise for the reader.
