I am very confused about the following:
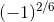
whenever I put in into wolfram alpha the answer it gives me is "indeterminate", is it not possible to simplify fractional exponents or something? if the exponent is 2/6 can i simplify it to 1/3 and get -1 as the answer? Provided I'm working with real numbers.
What I put in wolfram alpha was "(-1)^(1/3) real numbers" to which it answered "-1", then when I tried "(-1)^(2/6) real numbers" it answered "indeterminate".