Drawing a Right Triangle With Legs Not Parallel to x/y Axes?

Question

I have been presented with an interesting problem. How can I decide whether a right triangle with given side lengths can be placed (with integer coordinate vertices) on a Cartesian plane so that the legs are not parallel to the x or y axes?

I'm a little stumped as to how the lengths come into play. I figured I would just be considering the slopes of the legs, and whether they were 0 or undefined. Also, try as I might, I can't make a sketch of a triangle that obeys this non-parallel alignment specification.

Any ideas?

Answer 1

Note that the length of a segment whose vertices have integer coordinates are a number that can be written as $$\sqrt{a^2+b^2}$$ where $a$ and $b$ are integers.

Perhaps you find useful some background about Pythagorean triples.

Answer 2

If the sides are $a,b,c$ as usual, the condition requires that $a,b$ are themsleves hypothenuses of integer right triangles, i.e. $a^2=x^2+y^2$ and $b^2=u^2+v^2$ for certain nonzero(!) integers $x,y,u,v$. Since the $b$ edge is rotated by $90^\circ$ against the $a$ edge, these two right triangles are similar. That means that they are both integer multiples of a smaller, primitive right triangle. That is: We need a Pythagorean triple $r^2+s^2=t^2$ such that $t$ is a common divisor of $a$ and $b$. Thus you need to check if $\gcd(a,b)$ is an integer multiple of a number that occurs as hypothenuse of a Pythagorean triple. This is equivalent to the existence of a prime $p\equiv 1\pmod 4$ with $p\mid a$ and $p\mid b$.

Example: $a=78$, $b=104$, $c=130$ can be used as desired. Note that $\gcd(a,b)=26$ is a multiple of the prime $13\equiv 1\pmod 4$. We find a solution of $13^2=u^2+v^2$, namely $u=12, v=5$. This allows us to use $C=(0,0)$, $B=(6u,6v)=(72,30)$, $A=(8v,-8u)=(40,-96)$.

Answer 3

Here's an example of a right triangle with integer coordinates at every vertex and legs that are not parallel to either coordinate axis:

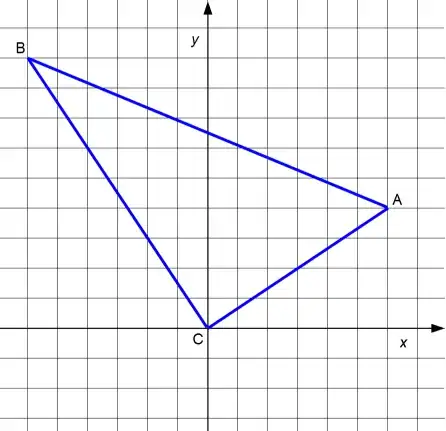
The vertices of this triangle are $A=(6,4),$ $B=(-6,9),$ and $C=(0,0).$

Now to find out whether a right triangle with given side lengths can be placed with all three vertices at integer coordinates, let's first try to determine what right triangles can be constructed on integer coordinates and what possible sets of lengths their sides can have. Then we can ask whether the given set of side lengths is one of those possible sets.

First of all, the three side lengths have to satisfy the Pythagorean formula. List the lengths in order of increasing size, so the lengths are $AC,$ $BC,$ and $AB$ with $AC \leq BC < AB.$ Then it must be true that $(AC)^2 + (BC)^2 = (AB)^2.$ If this is false, we do not even have a right triangle.

Now suppose we have three leg lengths as described in the previous paragraph. Without loss of generality, we can simplify our visualization and calculations by considering only triangles that (like the one in the figure) have a right angle at $C=(0,0),$ vertex $A$ in the first quadrant of the plane ($x>0,y>0$), and vertex $B$ in the second quadrant ($x<0,y>0$). Any other right triangle with integer coordinates can be translated an integer distance up or down and an integer distance right or left so that its right-angled vertex is at $(0,0),$ then (if needed) rotated by $90,$ $180,$ or $270$ degrees so that the other two vertices are in the first two quadrants, and then (if needed) "flipped" (reflected) around the $y$ axis so that the leg in the first quadrant is the shorter one.

So for the general case, let $A=(x_A,y_A),$ $B=(x_B,y_B),$ and $C=(0,0),$ where $x_A,$ $y_A,$ $x_B,$ and $y_B$ are all integers, $x_A>0,$ $y_A>0,$ $x_B<0,$ and $y_B>0$ as in the figure. The squares of the lengths of the two legs are then $(AC)^2=x_A^2+y_A^2$ and $(BC)^2=x_B^2+y_B^2.$

Right away this tells us something about the possible lengths of sides: the length of each leg is the square root of an integer. But not all integers are sums of squares of integers, so only some square roots of integers are possible side lengths. To know if an integer $N$ is a sum of squares, find the prime factorization of $N.$ If no prime of the form $4k+3$ has an odd exponent in that factorization, $N$ is a sum of two squares. This is due to a theorem of Fermat as explained here. Euler's proof of this theorem also gives some useful techniques to help find possible pairs of squares.

For the given set of side lengths of a triangle, then, let's determine whether $AC^2$ is the sum of two squares. If it is not, we can stop right away; the triangle's vertices cannot all have integer coordinates. (For this step we just need the prime factorization of $AC^2.$ Let's examine leg $AC$ a little closer before we actually look for the two squares.)

The slope of the leg $AC$ is $y_A/x_A.$ Since $y_A$ and $x_A$ are both integers, we can reduce this fraction to lowest terms, that is we can write $$\frac{y_A}{x_A} = \frac qp$$ where $p$ and $q$ are integers that have no common divisor, that is, $\gcd(p,q) = 1.$ This means $x_A=mp$ and $y_A=mq$ for some integer $m$ and $(p,q)$ is the point on the leg $AC$ with integer coordinates closest to $C.$ In the example in the figure, $(p,q)=(3,2).$

Since $(p,q)$ is on the leg $AC,$ the point $(-q,p)$ ($(-2,3)$ in the figure) is on the leg $BC,$ perpendicular to $AC.$ Moreover, $(-q,p)$ is the point on $BC$ with integer coordinates that is closest to $(0,0).$ Any other point on the line $BC$ that has integer coordinates must have coordinates that are just $(-q,p)$ scaled up by some integer factor. In order for $B$ to be at integer coordinates, then, we must be able to write $x_B=-nq$ and $y_B=np$ for some integer $n.$

So we can say this about the legs of the triangle: there exist positive integers $m,$ $n,$ $p,$ and $q$ such that $\gcd(p,q) = 1,$ $$\begin{eqnarray}(AC)^2 &=& (mp)^2 + (mq)^2 &=& m^2(p^2 + q^2), \mbox{ and}\\ (BC)^2 &=& (np)^2 + (nq)^2 &=& n^2(p^2 + q^2).\end{eqnarray}$$

In the case of a triangle with sides $AC = 2\sqrt{13},$ $BC = 3\sqrt{13},$ and $AB = 13,$ like the one in the figure, we can then look for two squares of positive integers whose sum is $(AC)^2 = 52.$ The only choice (apart from the order in which we list the squares) is $52 = 6^2 + 4^2.$ This gives us $m=2,$ $p=3,$ and $q=2,$ as illustrated in the figure. Now we need to check that we can find an integer $n$ such that $(BC)^2 = n^2(p^2 + q^2).$ We find that $n=3,$ so we know we can place all vertices of the triangle at integer coordinates, and moreover we have enough information to find one such set of coordinates.

In other cases there is a pitfall we must avoid. Suppose, for example, that $AC=5\sqrt{5},$ $BC=12\sqrt{5},$ and $AB=13\sqrt{5}.$ Then $(AC)^2 = 125 = 11^2 + 2^2,$ from which we get $m=1,$ $p=11,$ and $q=2.$ But we cannot find an integer $n$ such that $(BC)^2 = 720 = n^2(11^2 + 2^2).$ Yet we can place vertices of a triangle with these three side lengths at integer coordinates: $A=(10,5),$ $B=(-12,24),$ and $C=(0,0).$

It matters which two squares we find whose sum is $(AC)^2.$ We could have written $(AC)^2 = 125 = 10^2 + 5^2,$ and then we would have $m=5,$ $p=2,$ and $q=1.$ We would then easily find that $(BC)^2 = 720 = 12^2(2^2 + 1^2).$

In order to find suitable pairs of squares, we first find the largest square $m^2$ that divides $(AC)^2,$ so we can write $(AC)^2 = m^2 r$ where $r$ has no square factors. In fact, if $(AC)^2$ is the sum of two squares, then the prime factorization of $r$ has at most one factor of $2,$ at most one factor of any prime of the form $4k+1,$ and no other factors, and so there are integers $p$ and $q$ such that $r = p^2 + q^2.$ Moreover, for any values of $m',$ $p',$ and $q'$ that we could choose so that $(AC)^2 = m'^2 (p'^2 + q'^2),$ we will find that $p^2 + q^2$ is a divisor of $p'^2 + q'^2$ and that the quotient is the square of an integer. (This follows from facts used in counting the number of pairs of squares with the desired sum.) So if we can find an integer $n'$ such that $(BC)^2 = n'^2 (p'^2 + q'^2),$ we can find an integer $n$ such that $(BC)^2 = n^2 (p^2 + q^2).$

So if $(AC)^2$ is the sum of two squares, write $(AC)^2 = m^2 r$ where $m$ is an integer and $r$ is an integer with no square factors, and write $r = p^2 + q^2$ where $p$ and $q$ are integers. If it is possible to place the vertices of a triangle with the desired side lengths using only integer coordinates, then $(BC)^2/(p^2 + q^2)$ will be the square of an integer $n,$ and we will be able to write $(BC)^2 = n^2(p^2 + q^2)$ and find integer coordinates for all vertices of the desired triangle. But if $(BC)^2/(p^2 + q^2)$ is not the square of an integer, then it is not possible to draw a triangle with the desired side lengths using only integer coordinates for the vertices.