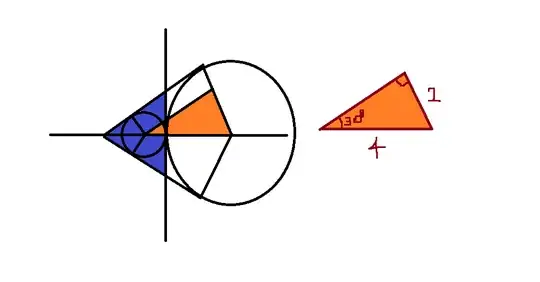Problem : Show that the common tangents to circles $x^2+y^2+2x=0$ and $x^2+y^2-6x=0$ form an equilateral triangle.
Solution :
Let $C_1 : x^2+y^2+2x=0$
here centre of the circle is $(-1,0) $ and radius 1 unit.
$C_2:x^2+y^2-6x=0$
here centre of the circle is $(3,0) $ and radius 3 units.
But how to proceed to prove that the tangents form equilateral triangle please suggest thanks.
Clearly the $Y$ axis (i.e. $x=0$) is a common tangent. Let $y=mx+c$ be the equation of the other common tangent(s). Then we need both the quadratics $$x^2+(mx+c)^2+2x=0 ; \qquad x^2+(mx+c)^2-6x=0$$
to have zero discriminant (why?). This gives us the conditions $$(cm+1)^2=(m^2+1)c^2; \qquad (cm-3)^2=(m^2+1)c^2$$
Solving these, we have $\pm\sqrt3 y=x+3$ as the other tangents. Quite obviously the intersection points are then $(-3, 0), (0, \pm \sqrt3)$ and it easily follows that the distance between any two vertices is $\sqrt{3^2+3}=2\sqrt3$.
The two circles are in homothetic position with respect to the center $H=(-3,0)$. Drawing a tangent $t$ from $H$ to the smaller circle we obtain a right triangle with hypotenuse $2$ and one leg $1$. It follows that $t$, which is a common tangent to both circles, makes an angle $30^\circ$ with the $x$-axis, and so does the other tangent from $H$. The third common tangent is vertical.
Can it be proved by elementary geometry?
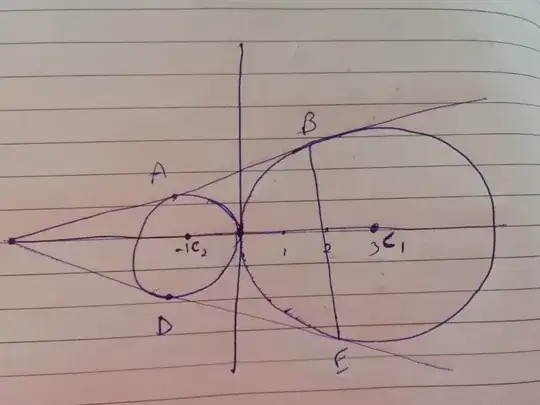
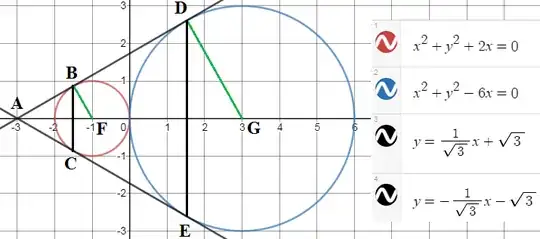
Suppose there are two circles $C_1$ and $C_2$ having respective radii $r_1$ and $r_2$, such that $r_1>r_2$, and respective centers $O_1$ and $O_2$.
Draw line $O_1O_2$ and a common external tangent which intersects circle 1 at $P_1$, circle 2 at $P_2$. These intersect at a point $Q$ such that $O_2$ lies between $O_1$ and $Q$. Draw radii $O_1P_1$ and $O_2O_P$ which are perpendicular to $P_1P_2$, thus parallel to one another. Thereby, triangles $O_1P_1Q$ and $O_2P_2Q$ are similar right triangles. From the proportionality of correspondung sides we then have:
$\frac{s+r_1+r_2}{r_1}=\frac{s}{r_2}$
$s=\frac{r_2(r_1+r_2)}{r_1-r_2}$
where $s$ is the length of line segment $O_2Q$.
When we put $r_1=3, r_2=1$ this gives $s=2$ so that the right triangle $O_2P_2Q$ has a hypoteneuse twice as long as one leg. Then angle $O_2QP_2$ opposite this leg measures $30°$.
Now draw all three common tangents. They form an isosceles triangle enclosing the smaller circle, whose apex angle at $Q$ measures twice the angle $O_2QP_2$, or $60°$. The triangle is thereby certified equilateral.
Orange triangle is half of equilateral triangle. Then Blue is equilateral triangle.
The figure will be something like this. Let the external point be $P$ and centres be $c_1$ and $c_2$. We have to prove that triangle $\Delta PBE$ is equilateral.
We know that $PB=PE$ and thus $\angle PBE=\angle PEB$. If we prove that $\angle EPB = 60^{\circ}$, then we will be able to prove that $\Delta PBE$ is an equilateral triangle.
Join $AC_2, DC_2, BC_1$ and $EC_2$. By observing carefully, you will be able to see that $\Delta PAC_2$ and $\Delta PBC_1$ are similar by angle-angle similarity.
So, $$\frac{AC_2}{PC_2}=\frac{BC_1}{PC_1} $$
We can find the radius by using the equation and you know that $C_1C_2$ is equal to $4$ units from the figure. Now you will be able to find length of $PC_1$ which comes out to be $6$ units.
Now, let $\angle BPE=\theta$. So $\angle C_1PB=\frac{\theta}{2}$.
$$\sin \frac{\theta}{2}=\frac{BC_1}{PC_1}=\frac{1}{2} \implies \frac{\theta}{2}=30 \implies \theta = 60$$
This proves that triangle $\Delta PEB$ is equilateral triangle.
More systematic and direct method!
Tangent line to $y=f(x)$ at the point $(x_0,y_0)$ is: $$y=y_0+y'(x_0)(x-x_0).$$
Let $(x_1,y_1)$ and $(x_2,y_2)$ be the tangent points of the common increasing tangent line to the circles $x^2+y^2+2x=0$ and $x^2+y^2-6x=0$, respectively.
Equate the slopes and intercepts of the tangent line: $$\begin{cases}y'(x_1)=y'(x_2)\\ y_1-x_1y'(x_1)=y_2-x_2y'(x_2)\end{cases} \Rightarrow \begin{cases}\frac{-x_1-1}{\sqrt{-x_1^2-2x_1}}=\frac{-x_2+3}{\sqrt{-x_2^2+6x_2}}\\ \frac{-x_1}{\sqrt{-x_1^2-2x_1}}=\frac{3x_2}{\sqrt{-x_2^2+6x_2}}\end{cases}$$ Divide $(1)$ by $(2)$ to find: $$x_1=\frac{3x_2}{3-4x_2}$$ Substitute it to $(2)$: $$\frac{x_1^2}{-x_1^2-2x_1}=\frac{9x_2^2}{-x_2^2+6x_2} \Rightarrow \frac{9x_2^2}{15x_2^2-18x_2}=\frac{9x_2^2}{-x_2^2+6x_2} \Rightarrow x_2=1.5 \Rightarrow x_1=-1.5.$$
Hence, the tangent line is: $$y=\frac1{\sqrt{3}}x+\sqrt{3} \Rightarrow \tan \alpha=\frac1{\sqrt{3}} \Rightarrow \alpha=30^\circ.$$ Note: Similarly, you can find the decreasing tangent line.
Refer to the diagram (for verifying other given answers and finding more methods):
