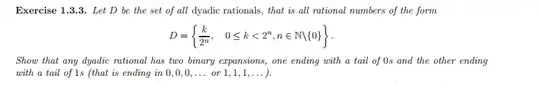
Completely stuck on this exercise! Hints and a starting point would be greatly appreciated. Nor do I see why is $x \in [ 0,1] \setminus D$ do not have $2$ binary expansions.
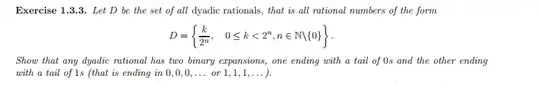
Completely stuck on this exercise! Hints and a starting point would be greatly appreciated. Nor do I see why is $x \in [ 0,1] \setminus D$ do not have $2$ binary expansions.
Note: $\frac{1}{2^i}+\frac{1}{2^{i+1}}+\cdots=\frac1{2^{i-1}}$.
Also dyadic rationals have a terminating binary expansion.
So you can trade in the last $1$ in the terminating representation for a $0$ in that place followed by a tail of all $1$s.
E.g., (binary representations): $.00101=.00100111111111...$