2

Can someone help me with computing the simplicial homology of the following space, and also clarify why it is a delta complex in the first place:

enter image description here

(The picture means that the edges are identified in the given orientation, also please note that the triangle is a solid triangle).

Thanks in advance!

Najib Idrissi
  • 56,269
Hajime_Saito
  • 1,855
  • In what way do the triangle represent a space? Which are the elements and the open sets? – Lehs Oct 08 '14 at 14:44
  • @Lehs http://en.wikipedia.org/wiki/Simplicial_complex – Najib Idrissi Oct 08 '14 at 14:46
  • @Najib: OK, I see. Thank you! – Lehs Oct 08 '14 at 14:48
  • @NajibIdrissi: Can you please clarify why the picture as given does not give a delta complex structure on the space? – Hajime_Saito Oct 08 '14 at 14:55
  • Assuming you consider the space as one of each 2-cell, 1-cell and 0-cell, one of the faces of the 2-cell would be the 1-cell but going in the wrong direction. This isn't allowed in the definition of a $\Delta$-complex. Basically: you can only identify edges if they are ordered in the same direction when you consider the standard simplex as $[0,1,\dots, n]$ – Najib Idrissi Oct 08 '14 at 14:56
  • (And you cannot go around that restriction by formally adding the edge in the opposite direction as a 1-cell, because a point must lie in the interior of exactly one cell). – Najib Idrissi Oct 08 '14 at 14:59
  • @NajibIdrissi: Sorry to disturb you again, but can you kindly give me the definition of a delta complex, or suggest a proper reference for it, other than Hatcher? I think I am confused with the definition, because I can't understand your reasoning above. – Hajime_Saito Oct 08 '14 at 15:02
  • 1
    Hm, check this thread out (I don't know alternatives myself). I'm going to edit my answer to explain better why the original isn't a $\Delta$-complex. – Najib Idrissi Oct 08 '14 at 15:08

1 Answers1

2

I think the best way is to subdivide the triangle like that:

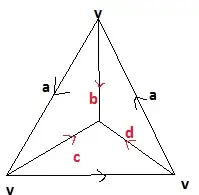
enter image description here

The arrows in red aren't identifications: I included them to make the Delta-complex structure clear. Then you get a Delta-complex with three 2-cells, four 1-cells and one 0-cell. Computing the homology of this space is a simple matter of linear algebra, which I'll let you do.

(By the way, if you know cellular homology, the answer would be immediate)

Why is the original not a $\Delta$-complex? Number the vertices of the standard $2$-simplex $\Delta^2 = [0,1,2]$ starting from the bottom left and counter-clockwise. In the quotient space where you identify all the $a$, the edge $[0,2]$ will be the edge $a$ but going in the reverse direction, that is to say $-a$. But $-a$ is not a 1-cell; $a$ is. In the definition of a $\Delta$-complex, all the faces of a cell must again be a cell, and the ordering of the vertices matter. In this case the face $[0,2]$ (the $d_1$ face if it makes sense) will not be one of the $1$-cell, it will be the opposite cell.

Najib Idrissi
  • 56,269