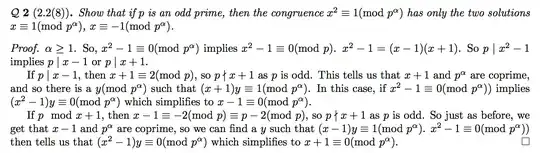In the $p | x - 1$ case, I'm a little confused about some of the latter steps; in particular, how does knowing that
$$\exists y \ s.t. (x+1)y \equiv 1\pmod{p^{\alpha}}$$
tell us that
$$(x^2 - 1)y \equiv 0\pmod{p^{\alpha}}$$
and how does this simplify to
$$x - 1 \equiv 0\pmod{p^{\alpha}}?$$
Thanks.
Personally, I feel the proof is formulated a bit awkwardly; some of the implications are, as you stated, not quite clear.
In your first two congruences, you do not actually need $y$. The existence of your $y$ is merely a side-product of the statement that $x+1$ and $p^\alpha$ are coprime.
This does not immediately yield $p^\alpha|(x^2-1)y$. Note that in your proof the line is "In this case, if $(x^2-1)y=0 \mod p^\alpha$, ..."
So this is another assumption - it is actually equivalent to your proposition (since $GCD(y,p)=1$).
To gain $x-1|p^\alpha$, we need the above fact that $GCD(y,p^\alpha)=GCD(x+1,p^\alpha)=1$.
Using that, the relation $p^\alpha|(x^2-1)=(x+1)(x-1)y$ simplifies directly to $p^\alpha|x-1$, which is what you want to show.
Frankly, looking at your proof, I am not entirely sure what the point of introducing $y$ is. It doesn't hurt, sure, but I cannot see how it makes anything easier, either.
Below is an alternative proof, using some algebra:
By this question, the multiplicative group of units modulo $p^n$ can always be embedded in a field, and an equation with degree $k$ and coefficients in a field has at most $k$ solutions in that field. Q.E.D.
Hope this helps.
