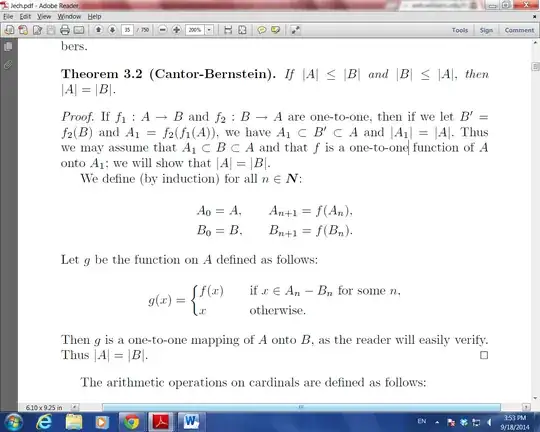
I have a problem with the proof of Cantor-Bernstein Theorem here below:
Take $A = (0,1)$ and $B = (0,\frac{1}{2})$. Then, $f(X) = \frac{x}{2}$ is a one to one function from $A$ to $B$ and from $B$ to $A$. So define $f_1 = f_2 = \frac{x}{2}$ (with the appropriate domaints).
I have tried to apply the proof on these sets but I seem not to be able following.
Can anyone describe what will happen to these sets during the proof?
Or, if it is easier, how can one be sure that the function $g$ defined in the proof is one-to-one and onto?
Thank you.