Showing Schlaefli integral satisfies Legendre equation

Question

The integral representation of Legendre functions is $P_ν(z)=\frac{2^{-\nu}}{2\pi i} \oint_Γ\frac{(w^2−1)^\nu}{(w−z)^{\nu+1}} dw$. I'm trying to show that this satisfies Legendre's equation.

When I take the derivatives and plug it into the equation, I just get a nasty expression with nasty integrals times functions of z. I don't see how I can combine any of the terms, since they have different powers of z, and all the integrals look different. $P'_ν(z)=\frac{2^{-\nu}}{2\pi i} \oint_Γ\frac{(w^2−1)^\nu(\nu+1)}{(w−z)^{\nu+2}} dw$ and $P'_ν(z)=\frac{2^{-\nu}}{2\pi i} \oint_Γ\frac{(w^2−1)^\nu(\nu+1)(\nu+2)}{(w−z)^{\nu+3}} dw$ So the expression is $$(1−z^2)\oint_Γ\frac{(w^2−1)^\nu(\nu+2)}{(w−z)^{\nu+3}} dw−2z \oint_Γ\frac{(w^2−1)^\nu}{(w−z)^{\nu+2}} dw+ν\oint_Γ\frac{(w^2−1)^\nu}{(w−z)^{\nu+1}} dw $$ Where I factored out a $\frac{2^{-\nu}(\nu+1)}{2\pi i}$ from each of the terms. Which I need to somehow show is equal to zero. I tried to collect all the integrals together, hoping they would combine together to give me a nice term. At first I was hoping it would give me $\frac{d}{dw}$ of the integrand, so I could just use Cauchy's theorem to show that the integral is zero. But the terms didn't seam to collect that way.

Oh and this integrand has branch points $\pm 1,z$, we take a cut between $-1$ and $-\infty$ along the negative real axis, and some cut between 1 and $z$. The contour $\Gamma$ is taken around a curve positively enclosing 1,$z$ (intersecting the real axis to the right of $-1$ as it must).

Answer 1

The question contains the definition \begin{equation*} P_ν(z)=\frac{2^{-\nu}}{2\pi i} \oint_\Gamma \frac{(w^2−1)^\nu}{(w−z)^{\nu+1}} dw \end{equation*}

Arfken$^1$, Ch12 Legendre Functions, Section 12.4 Alternate Definitions of Legendre Polynomials, gives, as part of (12.69), that

\begin{equation*} P_n(z)=\frac{2^{-n}}{2\pi i} \oint \frac{(t^2−1)^n}{(t−z)^{n+1}} dt \end{equation*}

and says that the contour encloses the point $t=z$.

The above integral for $P_n(z)$, is called the Schlaefli integral, here I use it for integers ‘n’, but it can be extended to non integral values of $P's$ index. A diagram should not really be required here, it’s such a simple idea. We have a closed contour in the complex t-plane, enclosing the point ‘z’.

Using $P_n(z)$ rather than $P_\nu(z)$ and substituting into Legendre's equation in the form

\begin{equation*} (1-z^2)P_n^{\prime \prime}(z)-2zP_n^\prime(z) +n(n+1)P_n(z)=0 \end{equation*} gives \begin{align*} \mathbf{A}&=(1-z^2)P_n^{\prime \prime}(z)-2zP_n^\prime(z) +n(n+1)P_n(z) \\ &=\frac{2^{-n}}{2\pi i} \oint \left[ [(1-z^2) \frac {d^2 }{dz^2 } \frac {(t^2-1)^n }{ (t-z)^{n+1}} ] -[2z\frac {d }{dz } \frac {(t^2-1)^n }{ (t-z)^{n+1}}] +[n(n+1)\frac {(t^2-1)^n }{ (t-z)^{n+1}}]\right]~dt \end{align*}

Using \begin{align*} \frac {d }{dz } \frac {(t^2-1)^n }{ (t-z)^{n+1}}&=\frac {d }{dz } (t^2-1)^n (t-z)^{-n-1} \\ &=(-n-1)(t^2-1)^n (t-z)^{-n-2} (-1) \\ &=\frac { (n+1)(t^2-1)^n}{ (t-z)^{n+2}} \\ \frac {d^2 }{dz^2 } \frac {(t^2-1)^n }{ (t-z)^{n+1}}&= \frac {d }{dz } \frac {d }{dz } \frac {(t^2-1)^n }{ (t-z)^{n+1}} \\ &=\frac { (n+1)(n+2)(t^2-1)^n}{ (t-z)^{n+3}} \\ \end{align*} \begin{align*} \mathbf{A}=\frac{2^{-n}}{2\pi i} &\oint ( \left[\frac { (1-z^2)(n+1)(n+2)(t^2-1)^n}{ (t-z)^{n+3}}\right] \\ &-~~\left[\frac {2z (n+1)(t^2-1)^n}{ (t-z)^{n+2}} \right] \\ &+~~\left[\frac {n (n+1)(t^2-1)^n}{ (t-z)^{n+1}} \right] )~dt\\ =\frac{2^{-n}}{2\pi i} &\oint \frac { (n+1)(t^2-1)^n}{ (t-z)^{n+3}} \left[ ((n+2)(1-z^2))-2z(t-z)+n(t-z)^2 \right] ~dt \end{align*}

Inside the square brackets we have \begin{equation*} (n+2-nz^2-2z^2)-(2zt-z^2)+(nt^2-2znt+nz^2)=nt^2-2znt-2zt+n+2\end{equation*}

Hence, we have a main result \begin{equation*} \mathbf{A}=\frac{2^{-n}}{2\pi i}(n+1)\oint \frac { (t^2-1)^n}{ (t-z)^{n+3}}[nt^2-2znt-2zt+n+2]~dt \tag{1} \end{equation*}

Now \begin{align*} \frac{ d}{dt }\left[ (t^2-1)^{n+1} (t-z)^{-n-2} \right]&=[(n+1)(t^2-1)^n2t ](t-z)^{-n-2} \\ &+(t^2-1)^{n+1}[-(n+2)(t-z)^{-n-3}] \\ &= \frac{(t^2-1)^n ~~~~}{(t-z)^{n+3} } [ ~[(n+1)2t(t-z)~]-[~(n+2)(t^2-1)~] ~]\\ \end{align*}

Processing the symbols inside square brackets \begin{align*} [(n+1)2t(t-z)~]&=(n+1)(2t^2-2zt) =2nt^2+2t^2-2znt-2zt \\ -[~(n+2)(t^2-1)~] &=n+2-nt^2-2t^2 \end{align*} Adding the right-hand sides of the above two equations, gives \begin{equation*} [nt^2-2znt-2zt+n+2] \end{equation*}

So, \begin{equation*} \frac{d}{dt} \frac { (t^2-1)^{n+1}}{ (t-z)^{n+2}}=\frac { (t^2-1)^n}{ (t-z)^{n+3}}[nt^2-2znt-2zt+n+2]\end{equation*}

Hence, we can express $\mathbf{A}$, see the result in (1), as

\begin{equation*} \mathbf{A}=\frac{2^{-n}}{2\pi i}(n+1)\oint \frac{d}{dt} \left[ \frac { (t^2-1)^{n+1}}{ (t-z)^{n+2}}\right]~dt \tag{2} \end{equation*}

Our $\mathbf{A}$, as given above, has the value zero. Upon completing a closed contour the function \begin{equation*} \frac { (t^2-1)^{n+1}}{ (t-z)^{n+2}} \end{equation*} returns to it's original value,and the integral is zero.

Knowing that $\mathbf{A}=0$, we may say that the function \begin{equation*} P_n(z)=\frac{2^{-n}}{2\pi i} \oint \frac{(t^2−1)^n}{(t−z)^{n+1}} dt \end{equation*}

satisfies Legendre's equation, \begin{equation*} (1-z^2)P_n^{\prime \prime}(z)-2zP_n^\prime(z) +n(n+1)P_n(z)=0 \end{equation*}

The Schlaefli integral, satisfies Legendre’s equation.

Reference:

1, George Arfken, Mathematical Methods For Physicists, Second Edition, Academic Press (1970).

Answer 2

I figured it out, if you put in $(1-z^2) = -(w^2-1) + 2w(w-z) - (w-z)^2$ and $z = w -(w-z)$ and do the algebra, it comes to $ \frac{d}{dw} \Big[ \frac{(w^2-1)^{\nu+1}}{(w-z)^{\nu+2}}\Big]$ so you can evaluate the integral, by evaluating $\frac{(w^2-1)^{\nu+1}}{(w-z)^{\nu+2}}$ around $\Gamma$ but it is a closed curve so it must vanish. I think that proves it, any thoughts?

Answer 3

For non-integral ‘$\nu$’, substituting the Schlaefli integral form of the function $P_\nu(z)$

\begin{equation*} P_\nu(z)=\frac{2^{-\nu}}{2\pi i} \oint_Γ\frac{(t^2−1)^\nu}{(t−z)^{\nu+1}} dt \tag{1} \end{equation*}

into the left-hand side of Legendre’s equation

\begin{equation*} (1-z^2)P_\nu^{\prime \prime}(z)-2zP_\nu^\prime(z) +\nu(\nu+1)P_\nu(z)=0 \tag{2} \end{equation*}

would lead to

\begin{align*} &(1-z^2)P_\nu^{\prime \prime}(z)-2zP_\nu^\prime(z) +\nu(\nu+1)P_\nu(z)\\ =&\frac{2^{-\nu}}{2\pi i}(\nu+1)\oint_\Gamma \frac { (t^2-1)^\nu}{ (t-z)^{\nu+3}}[\nu t^2-2z\nu t-2zt+\nu+2]~dt \\ =&\frac{2^{-\nu}}{2\pi i}(\nu+1)\oint_\Gamma \frac{d}{dt} \left[ \frac { (t^2-1)^{\nu+1}}{ (t-z)^{\nu+2}}\right]~dt \tag{3} \end{align*}

Call the right-hand side of (3), $\mathbf{\tilde{A}}$

\begin{equation*} \mathbf{\tilde{A}}=\frac{2^{-\nu}}{2\pi i}(\nu+1)\oint_\Gamma \frac{d}{dt} \left[ \frac { (t^2-1)^{\nu+1}}{ (t-z)^{\nu+2}}\right]~dt \tag{4} \end{equation*}

If, $\mathbf{\tilde{A}}=0$, then the Sclaefli integral satisfies the Legendre equation.

See my first answer, to this question, dated Oct 7 2022, Showing Schlaefli integral satisfies Legendre equation . There I analyse, starting with $P_n(z)$ not $P_\nu(z)$, but the derivations can easily be adapted, changing ‘$n$’s to ‘$\nu$’s in the math, should do the trick, but only up to (2), after which there is material on $\mathbf{A}=0$. See (1) and (2) in particular.

For $\mathbf{\tilde{A}}$ to equal zero, we must have, for the multi-valued function $(t^2-1)^{\nu+1}/ (t-z)^{\nu+2}$

\begin{equation*} \left[ \frac { (t^2-1)^{\nu+1}}{ (t-z)^{\nu+2}}\right]_{t_1}^{t_2}=0 \end{equation*} where $t_1$ is considered the start of $\Gamma=\Gamma_1$, i.e. the start of our chosen contour, and $t_2$ is the end point of the same contour.

$\Gamma_1$." />

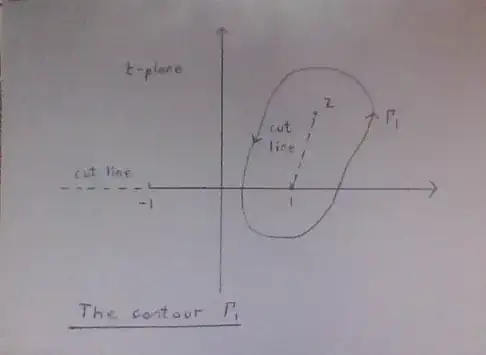
There is now described an Arfken$^1$ type closed contour, called $\Gamma_1$, which lies in the complex t-plane.

The t-plane contains a particular point called $z$, placed in the upper right quadrant. Special points are $t=+1$, $t=-1$, $t=z$. There are two cut-lines, the first from $t=1$ to $t=z$, the second from $t=-1$ to $t=-\infty$.

The closed contour $\Gamma_1$, encircles both the points $t=z$ and $t=+1$, but does not cross either of the two cut-lines. Hence the cut-line from $t=+1$ to $t=z$ is completely enclosed by $\Gamma_1$

The contour $\Gamma_1$ does not cross any cut-lines, hence it looks as if $t_2$ is the same point as $t_1$. It looks as if, it is not on some other sheet of a multi-sheeted construct. So we have, $\mathbf{ \tilde{A}}=0$.

Knowing that $\mathbf{ \tilde{A}}=0$ we may say that the function

\begin{equation*} P_\nu(z)=\frac{2^{-\nu}}{2\pi i} \oint_Γ\frac{(t^2−1)^\nu}{(t−z)^{\nu+1}} dt \end{equation*}

satisfies Legendre’s equation

\begin{equation*} (1-z^2)P_\nu^{\prime \prime}(z)-2zP_\nu^\prime(z) +\nu(\nu+1)P_\nu(z)=0 \end{equation*}

The Schlaefli integral, satisfies Legendre’s equation.

Reference

1, George Arfken, Mathematical Methods For Physicists, Second Edition, Academic Press (1970). See Ch12 Legendre Functions, Section 12.4 Alternate Definitions of Legendre Polynomials, Fig12.9.