Using integration by parts, show that $\displaystyle \int e^{2x} \sin x dx=\dfrac{1}{5}e^{2x}(2\sin x-\cos x)+c$

Question

I have the mark scheme in front of me, but there's something I don't understand.

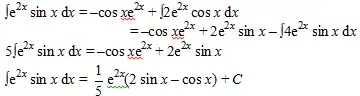
enter image description here

I don't understand how the markscheme goes from the 2nd line to the 3rd line. In my working, I'm on $-\cos x e^{2x}+(2 \sin xe^{2x}-\int4e^{2x}\sin x dx)$. The last integral is the same as the start, but with a constant - doesn't that put me in an infinite loop?

No. You're just solving an equation of the form $I=B-4I$ for $I$. — David Mitra, Sep 14 '14 at 09:21
http://math.stackexchange.com/questions/540295/integrate-eax-sinbx — lab bhattacharjee, Sep 14 '14 at 09:22

score 1 · Answer 1 · answered Sep 14 '14 at 09:26

There's no loop there: on the third line you have $$\int e^{2x}\sin x \mathrm{d}x=-\cos{xe^{2x}}+2e^{2x}\sin{x}-4\int e^{2x}\sin x \mathrm{d}x$$

This is just an equation of the form $x=y-4x$ where $$x=\int e^{2x}\sin x \mathrm{d}x,y=-\cos{xe^{2x}}+2e^{2x}\sin{x}$$ move the integral from the right hand side to the left one and then divide by 5

Using integration by parts, show that $\displaystyle \int e^{2x} \sin x dx=\dfrac{1}{5}e^{2x}(2\sin x-\cos x)+c$

1 Answers1