26

As I was just checking this 'child prodigy' out on Youtube, I stumbled upon this video, in which Glenn Beck asks the kid to do the following proof:

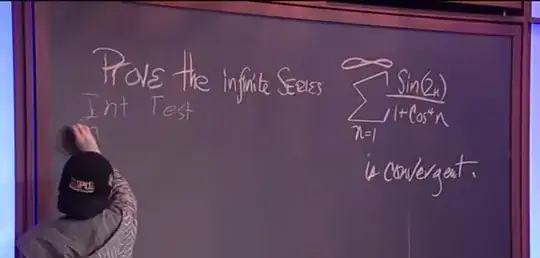
Further on, the kid starts sketching a proof (without a shadow of a doubt regarding the accuracy of his solution ) including the Integral Test. I don't know much about improper integrals since I just finished highschool, but this integral approach seemed, intuitively, pretty inaccurate to me since this is not a strictly decreasing function. Then I found this out from Wikipedia ! Conditions for the Integral Test.

Furthermore, the blunt assessment that the series are convergent seems dubious as well..Upon a few computations of my own(mostly partial sums) , I tend to believe that the series are, in fact, divergent .

Can anyone suggest a rigurous take on this problem (easy as it may seem to some amongst you) ?

Alexander Gruber
  • 28,037
Victor
  • 3,238
  • 12
    But the sum $$\sum_{n=1}^{\infty} \frac {\sin(2n)}{1+\cos^4(n)}$$ does not converge. Am I reading the chalk board wrong? – UserX Sep 09 '14 at 21:53
  • 2
    Haha, no! that's my contention as well – Victor Sep 09 '14 at 21:55
  • 1
    This is interesting indeed, as one should immediately see that the relevant integral diverges by oscillation (if they were not keen enough to notice that the partial sums do not converge). – Gahawar Sep 09 '14 at 22:05
  • 2
    Who came up with this question? I think the kid shouldn't be entirely blamed, but also whoever came up with the question. Wrong questions can trip up experienced mathematicians too, since some take shortcuts when they assume the result is true. – Fengyang Wang Sep 09 '14 at 22:13
  • Does it make any different whether this is asking whether $\frac{\sin(2n)}{1 +\cos^4(n)}$ has a limit as $n$ goes to $\infty$ (as opposed to whether the sum does)? (E.g., the limit of $1+\frac{1}{n}$ as $n$ goes to $\infty$ is $1$, but $\sum_{n=1}^\infty 1+\frac{1}{n}$ diverges.) Just wondering whether someone meant to ask one question but wrote a different one on the blackboard. – Joshua Taylor Sep 10 '14 at 04:16
  • Please keep your comments on topic. – Alexander Gruber Sep 10 '14 at 05:27
  • 1
    Why should the kid be blamed at all? He set up the integral correctly, and was making sensible first steps towards evaluating it when he was asked to stop working. There are some shortcuts he could have employed, but anybody could overlook those in two minutes. – Andrew Dudzik Sep 10 '14 at 05:54
  • Sort of embarrassing on his and the channel's part. – Aleksandar Oct 04 '15 at 20:35

3 Answers3

41

Yes the series is indeed divergent. A necessary condition for the series to be convergent is, that the sequence $$\frac{\sin(2n)}{1+\cos^4(n)}$$ tends to zero as $n\to\infty$. This, however, is not the case as $$\left|\frac{\sin(2n)}{1+\cos^4(n)} \right|\geq \left|\frac{\sin(2n)}{2}\right|$$ and $\sin(2n)$ obviously does not tend to $0$.

Rustyn
  • 8,474
Peter
  • 3,441
  • 1
    Thanks @Peter, this sorted out the pickle Mr. Beck put me in ! +1 – Victor Sep 09 '14 at 22:16
  • 5
    Well, to be fair, it's not completely obvious that $\sin(2n)$ does not tend to zero. To show that, notice that if $\lvert \sin(2n)\rvert <1/2$, then $\lvert\sin(2n+2)\rvert>1/2$ or $\lvert\sin(2n-2)\rvert>1/2$, because $2<2\pi/3$. – tomasz Sep 09 '14 at 22:26
  • The series is not convergent, it doesn't mean that it is divergent. – Felice Iandoli Sep 09 '14 at 22:32
  • 25
    I think it does exactly mean that. – Peter Sep 09 '14 at 22:35
  • @FeliceIandoli Perhaps you might want to look at his comparison test? –  Sep 09 '14 at 23:46
  • @Peter $\sum_{n\geq 1}(-1)^n$ is not convergent, but it is not divergent. To be divergent means that $\sum_{n\geq 1}a_n=\infty$, and for the former series you can't decide. – Felice Iandoli Sep 10 '14 at 07:57
  • @Committingtoaname I was only pedantic. Because I hate earing: "This series does not converge, so diverges". It is the same thing to say: "A limit of a sequence $a_n$ is not finite, so it is $\infty.$" The sequence could not to have a limit. – Felice Iandoli Sep 10 '14 at 08:06
  • 2
    @Felice: Well, it seems to be just a discussion about notation. For me 'divergent' means by definition 'not convergent'. (Wikipedia has actually the same definition of divergent: https://en.wikipedia.org/wiki/Divergent_series). So in my opinion, a bounded, not convergent series is still divergent, although it does not tend to infinity. – Peter Sep 10 '14 at 08:36
  • Ok, @Peter. It's just a discussion about notation. – Felice Iandoli Sep 10 '14 at 08:46
2

\begin{align} \sin(2n) &= 2\sin(n)\cos(n) = -\frac{\mathrm i}{2}\sum_{n=0}^\infty\frac{(2\mathrm in)^n - (-2\mathrm i n)^n}{n!} \\ &= -\frac{\mathrm i}2 \sum_{n=0}^\infty \frac{n^n(2^n(\mathrm i^n - \mathrm i^{3n}))}{n!} \\ &= -\frac12 \sum_{n=1}^\infty \frac{(2\mathrm in)^n(1 - (-1)^n)}{n!}. \end{align}

Noting $$\lim_{n\to\infty}\left|\frac{(2n)^n\mathrm i^{n+3}}{n!}\right| = \infty,$$ and that the radius of curvature is $\limsup_{n\to\infty}{(n!/(2n)^n)^{1/n}} = \lim{n\to\infty}(2n)^{-1} = 0,$ and that $$1 \le (1+\cos^4 n) \le 2,$$ it is evident that both the real and imaginary parts of the series $$\sum_{n=1}^\infty\frac{\sin 2n}{1+\cos^4 n}$$ diverge.

Similarly, the same is true of both real and imaginary parts of denominator. Hence the series neither converges nor diverges.

Accomplished by expressing $\sin(n)\cos(n)$ exponentially and implementing the exponential serial expansion. Similarly the denominator.

filmor
  • 549
user150282
  • 49
0

From divergence test it is obvious too that $\sum_{n=1}^\infty \frac{\sin(2n)}{1+\cos^4(n)}$ must diverge.

As, $$\lim_{n \rightarrow \infty}\frac{\sin(2n)}{1+\cos^4(n)} \neq 0.$$

kaka
  • 1,916