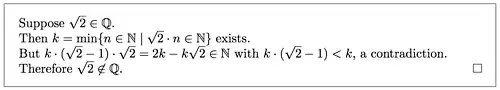4

I have found the following alternative proof online. Proof irrationality square root of 2

It looks amazingly elegant but I wonder if it is correct.

I mean: should it not state that $(\sqrt{2}-1)\cdot k \in \mathbb{N}$ to be able to talk about a contradiction?

Doesn anybody know who thought of this proof (who should I credit)? I couldn't find a reference on the web.

Community
  • 1
dietervdf
  • 4,644

2 Answers2

3

The proof goes back to at least Dedekind - being a special case of much more general results about conductor ideals. Here is a presentation bringing these concepts to the fore (but using nothing more than high-school algebra).

Theorem $\ $ Let $\;\rm n\in\mathbb N.\;$ Then $\;\rm r = \sqrt{n}\;$ is integral if rational.

Proof $\ $ Consider the set $\rm D$ of all the possible denominators $\rm d$ for $\rm r, \;$ i.e. $\;\rm D = \{\, d\in\mathbb Z \;:\: dr \in \mathbb Z\,\}$. Note $\rm D$ is closed under subtraction: $\rm\, d,e \in D\, \Rightarrow\, dr,\,er\in\mathbb Z \,\Rightarrow\, (d-e)\:r = dr - er \in\mathbb Z.\;$ Further $\rm d\in D \,\Rightarrow\, dr\in D\,$ since $\rm\, (dr)r = dn\in\mathbb Z \;$ by $\;\rm r^2 = n\in\mathbb Z.\;$ Therefore, invoking the Lemma below, with $\rm d $ the least positive element in $\rm D,$ we infer that $\;\rm d\,|\,dr \;$ in $\mathbb Z,\;$ i.e. $\rm\ r = (dr)/d \in\mathbb Z.\quad$ QED

Lemma $\ $ Suppose $\;\rm D\subset\mathbb Z \;$ is closed under subtraction and that $\rm D$ contains a nonzero element.
Then $\rm D \:$ has a positive element and the least positive element of $\rm D$ divides every element of $\rm D\:$.

Proof $\rm\,\ \ 0 \ne d\in D \,\Rightarrow\, d-d = 0\in D\,\Rightarrow\, 0-d = -d\in D.\, $ Hence $\rm D$ contains a positive element. Let $\rm d$ be the least positive element in $\rm D$. Since $\rm\: d\,|\,n \!\iff\! d\,|\,{-}n,\,$ if $\rm\, c\in D$ is not divisible by $\rm d$ then we may assume that $\rm c$ is positive, and the least such element. But $\rm\, c-d\,$ is a positive element of $\rm D$ not divisible by $\rm d$ and smaller than $\rm c$, contra leastness of $\rm c$. So $\rm d$ divides every element of $\rm D.\ $ QED

Remark $ $ The theorem's proof exploits the fact that the denominator ideal $\rm D$ has the special property that it is closed under multiplication by $\rm\: r\:.\ $ The fundamental role that this property plays becomes clearer when one learns about Dedekind's notion of a conductor ideal. Employing such yields a trivial one-line proof of the generalization that a Dedekind domain is integrally closed since conductor ideals are invertible so cancellable. This viewpoint serves to generalize and unify all of the ad-hoc proofs of this class of results - esp. those proofs that proceed essentially by descent on denominators. This conductor-based structural viewpoint is not as well known as it should be - e.g. even some famous number theorists have overlooked this. See my post here for further details.

Community
  • 1
Bill Dubuque
  • 282,220
  • Wow, this looks like heavy stuff :) – dietervdf Sep 04 '14 at 19:47
  • @dietervdf $ $ Both proofs can be understood by a bright high-school student. But the generalizations mentioned in the remark require knowledge of basic abstract algebra (esp. ideals). – Bill Dubuque Sep 04 '14 at 19:52
3

The proof is correct, but you could say it's skipping over a couple of steps: In addition to pointing out that $(\sqrt2-1)k\in\mathbb{N}$ (because $\sqrt2k\in\mathbb{N}$ and $k\in\mathbb{N}$), one might also want to note that $1\lt\sqrt2\lt2$, so that $0\lt\sqrt2-1\lt1$, which gives the contradiction $0\lt(\sqrt2-1)k\lt k$.

As for the source of the proof, you might try looking at the references in an article on the square root of 2 by Martin Gardner, which appeared in Math Horizons in 1997.

Barry Cipra
  • 81,321
  • Super! I'll look into those references. – dietervdf Sep 04 '14 at 20:09
  • But if $k \in \mathbb N$ such that also $\sqrt 2 k \in \mathbb N$, what prevents us to conclude with : $\sqrt 2 \in \mathbb N$ ? – Mauro ALLEGRANZA Sep 04 '14 at 20:11
  • Interesting point and true, but it doesn't seem any reason for a contradiction. – dietervdf Sep 04 '14 at 20:12
  • 1
    If $\sqrt 2 \in \mathbb N$ and we note that $1 < \sqrt 2 < 2$, we have a contradiction... Otherwise we have to say that $1 \le \sqrt 2 \le 2$, which implies : $\sqrt 2 = 1$ or $\sqrt 2 = 2$. But $1^2 = 1 \ne 2$ and also $2^2=4 \ne 2$. – Mauro ALLEGRANZA Sep 04 '14 at 20:16
  • Hey, that also looks cool – dietervdf Sep 04 '14 at 20:20
  • @dietervdf You won't find the historical source in Gardner's article since his references only go back to 1969, but the proof is much older than that. Someday I will probably write something on the history of this and closely related topics (which deserves to be much better known). – Bill Dubuque Sep 04 '14 at 20:38