7

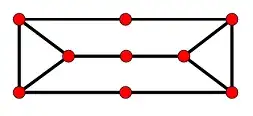
The property of the graph is the following: For any vertex, there is a hamiltonian path starting with this vertex, but the graph is not hamiltonian. The following graph is a small example: example graph

Important examples are hypohamiltonian graphs (deleting each vertex leads to a hamiltonian graph, but the graph is not hamiltonian ; for example the Petersen graph)

  • Is there a name for such graphs?
  • Which numbers of vertices are possible for such a graph?
  • Is there a knight graph with this property? (See mathworld knight graph for more details. I think the answer is no.)
DavidButlerUofA
  • 3,414
  • 18
  • 24
Peter
  • 86,576
  • The graph with the edges 1-2 , 1-4 , 1-6 , 2-3 , 3-5 , 3-8 , 4-6 , 4-9 , 5-8 , 5-9 , 6-7 , 7-8 has the desired property. Is it the smallest ? – Peter Aug 28 '14 at 23:12
  • 1
    Just to be clear: a hamiltonian path visits all the vertices once; a hamiltonian cycle visits all the vertices once and comes back to the start again; a graph is hamiltonian if it has a hamiltonian cycle. So you're saying that every vertex has a path starting there that goes to all the other vertices once, but none that come back to this vertex again. Right? – DavidButlerUofA Aug 28 '14 at 23:31
  • 1
    @Peter: I think the smallest example is $K_2$. – Steve Kass Aug 29 '14 at 00:49
  • 1
    @steve maybe, per definition, $K_2$ has the desired property, but of course, this trivial graph should not be considered. – Peter Aug 29 '14 at 10:37
  • @david exact that! The graph has no hamilton-cycle, but from any vertex, a hamilton path can be found. – Peter Aug 29 '14 at 10:39
  • If the graph is not allowed to have a 3-circle (triangle free graph), then the smallest besides the $K_2$ seems to be the following : $1-2$ , $1-9$ , $2-3$ , $2-7$ , $3-4$ , $3-10$ , $4-5$ , $4-8$ , $5-6$ , $6-7$ , $6-10$ , $7-8$ , $8-9$ , $9-10$ with $10$ vertices and $14$ edges. – Peter Aug 29 '14 at 10:42

1 Answers1

1

These are homogeneously traceable non-hamiltonian graphs.

See e.g. "On homogeneously traceable nonhamiltonian graphs" (Gary Chartrand, Ronald J. Gould, S. F. Kapoor, 1979). In this paper they "construct, for each integer $p > 9$, a homogeneously traceable nonhamiltonian graph of order $p$" and prove that there are none with 3 to 8 vertices.

It was abbreviated as NHHT in the 2007 paper "Nontraceable detour graphs" (DOI 10.1016/j.disc.2006.07.019):

The study of nonhamiltonian, homogeneously traceable graphs (NHHT graphs) was initiated by Skupień in 1975...

Nick Matteo
  • 9,316