I am trying to find the value of $\displaystyle\int_0^\infty\frac{(\log x)^2}{1 + x^2}\,dx$ using contour integration.
My approach:
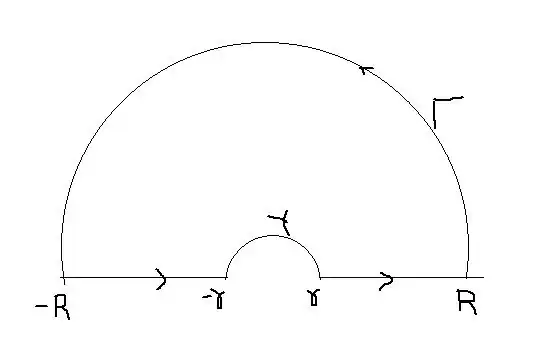
I have calculated the residue at z = $i$ and have shown that integration over small circle is equal to $0$.
However I am having trouble in establishing that $\int_\Gamma f(z) = 0$
The book that I am following states that to show that it is equal to zero it is sufficient to show that $\lim_{z \to \infty} zf(z) = 0$ But if I use this method then the limit tends to $\infty$ and not zero.
Am I applying any wrong concept ?