Can anyone please answer the following questions ?
1) $\int\left \lfloor{x}\right \rfloor dx$
2) $\int$ $ \left \lfloor{\sin(x)}\right \rfloor $ $dx$
3) $\int_0^2$ $\left \lfloor{x^2+x-1}\right \rfloor$ $dx$
4) $\int_o^\pi$ $\left \lfloor{x(1+\sin(\pi x)}\right \rfloor$
Also can anyone please make me understand the way in which to proceed in these types of sums?
$\left \lfloor{x}\right \rfloor$ is the floor function
Thanks
A related problem. I'll do number $(3)$. Note that for $n \in \mathbb{N} $ we have
$$ n \leq x < n+1 $$
$$ \implies n^2 \leq x^2 < (n+1)^2 $$
$$ \implies n^2+n-1 \leq x^2+x-1 < (n+1)^2 +(n+1)-1 $$
which yields
$$ \lfloor{ x^2+x-1} \rfloor = n^2+n-1, \quad n \leq x < n + 1 .$$
Now, we go back to the integral
$$ I = \int_{0}^{1}(-1) dx + \int_{1}^{2}(1) dx = 0. $$
Note: I believe You can generalize the above process for any polynomial $p(x)$.
$1)$ The area under the graph of $\lfloor{x}\rfloor$ is $0+1+2 +\cdots+(x-1)$ so $$\int{\lfloor{x}\rfloor} \, dx =\frac{x(x-1)}{2}$$ $2)$ The graph of $\lfloor{\sin(x)}\rfloor$ alternates between $0$ and $-1$ every $\pi$ values, so every $2\pi$ values the integral will $-1$. So $$\int\big\lfloor{\sin(x)}\big\rfloor \, dx = -\lfloor{\frac{x}{2\pi}}\rfloor-\frac{\operatorname{sgn}\big((x\bmod{2\pi}) - \pi\big)+1}{2}$$ $3)$ $$\int_{0}^{2}\Big\lfloor\left(x^{2}+x-1\right)\Big\rfloor \, dx\approx1.726$$ $4)$ $$\int_0^\pi \big\lfloor x(1+\sin(\pi x)\big\rfloor \, dx\approx4.530$$
I will show you how to perform the integral given by $3)$ on a slightly rough way.
We know that $p(x) = x^2 + x-1$ lies between $(-1,5)$ when $x \in (0,2)$ and, furthermore, $p$ is monotone increasing in this interval.
When applied to $p(x)$, the floor function gives us the greatest integer less than or equal to $x$, so it makes a good idea to compute for what values of $x$, $p(x)$ reach an integer value $p \in (-1,5)$. We have: \begin{array}{|c|c|} \hline p(x) & x \\ \hline -1 & 0 \\ 0 & \frac{1}{2} \left(-1+\sqrt{5}\right) \\ 1 & 1 \\ 2 & \frac{1}{2} \left(-1+\sqrt{13}\right) \\ 3 & 1/2 (-1 + \sqrt{17}) \\ 4 & 1/2 (-1 + \sqrt{21}) \\ 5 & 2 \\ \hline \end{array} where we have solved $p(x) = p^* = -1,0,\ldots,5,$ on each table entry.
Now, we can see that: $$\color{blue}{\int^2_0 \lfloor p(x) \rfloor \, \mathrm{d}x = \sum_{i=0}^5 (x^*_{i+1} -x^*_i) p^*_i}, $$ where $x^*_i $ are the corresponding values satisfying $p(x^*) = p^*$. I hope this gives you some ideas of what's going on.
Cheers!
I'm sure a plot of both $p(x)$ and $\lfloor p(x) \rfloor$ makes things clearer:
The floor function turns continuous integration problems in to discrete problems, meaning that while you are still "looking for the area under a curve" all of the curves become rectangles. In general, the process you are going to want to take will go something like this:
Consider the function (before taking the floor of it), and look at where the output is an integer. For instance, in your first example $f(x)=x$, $f(x)$ equals an integer when an integer is put in. The next step is to look at what happens between these points. Again considering your first example, for $1 \leq x < 2$, the floor function maps everything to 1, so you end up with a rectangle of width 1 and height 1. It is the areas of these rectangles you need to add to find the value of the integral (being careful to understand that rectangles below the x-axis have "negative areas").
In the case of the indefinite integrals you will end up with some summation since you don't know the bounds, on the others you should be able to find exact numerical answers.
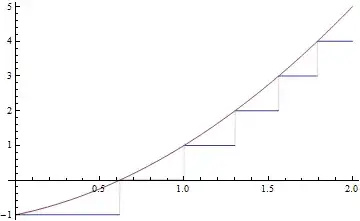
It seems to me that integrating the floor function gives you triangular numbers when the input is a whole number. So for those cases, you can use the triangular number formula but with $x-1$ instead of $x$ because the values are shifted to the right in this case.
$$\frac{(x-1)^2+(x-1)}2$$
Then to account for the portion of $x$ in between whole numbers, we do this:
$$\frac{(\lfloor x\rfloor-1)^2+(\lfloor x\rfloor-1)}2+(x-\lfloor x\rfloor)\lfloor x\rfloor$$
For negative integers, we have:
$$\frac{-(x-1)^2-(x-1)}2$$
And again we add on the non-integer portion:
$$\frac{-(\lfloor x\rfloor-1)^2-(\lfloor x\rfloor-1)}2-(x-\lfloor x\rfloor)\lfloor x\rfloor$$
It looks like the function for negative values of $x$ is the same as the function for positive values, but multiplied by $-1$. So if we want one function to be the answer for problem #1, we can have:
$$sgn(x)\left(\frac{(\lfloor x\rfloor-1)^2+(\lfloor x\rfloor-1)}2+(x-\lfloor x\rfloor)\lfloor x\rfloor\right)$$
Let $x_n$ be the successive values of $x$ where $f(x)$ takes an integer value (they can be obtained by solving $f(x)\in\mathbb Z$ and sorting). As $\left\lfloor f(x)\right\rfloor$ is piecewise constant, the antiderivative is piecewise linear, continuous, with a slope equal to $f(x_k)$.
If we start integrating at $x_0$, up to some $x_n$, the integral is the sum
$$\int_{x_0}^{x_n}\left\lfloor f(x)\right\rfloor dx=\sum_{k=0}^{n-1}f(x_k)(x_{k+1}-x_k).$$
And if we continue integrating to some $x$ that does not exceed $x_{n+1}$,
$$\int_{x_0}^x\left\lfloor f(x)\right\rfloor dx=\sum_{k=0}^{n-1}f(x_k)(x_{k+1}-x_k)+f(x_n)(x-x_n).$$
$$\lfloor sinx\rfloor $$ is equal to either 0 or 1 or -1, so integrating it should be simple
