Define the error associated with selecting a particular set of $A,B,C,D,E,F$ to be
$ \varepsilon_i = A x_i^2 + B x_i y_i + C y_i^2 + D x_i + E y_i + F $
This is the error for the $i$-th point $(x_i, y_i)$.
We want to minimize
$ J = \displaystyle \sum_{i=1}^N \varepsilon_i^2 $
To make this work we need to somehow normalize the set $A,B,C,D,E,F$. A good way to do this is to impose that
$ A + C = 1$
i.e. we take $C = 1 - A $
The error function is now
$J = \displaystyle \sum_{i=1}^N \left( A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right)^2 $
At the minimum of $E$, its partial derivatives with respect to $A, B, D, E, F$ are zero.
This leads to the following "normal" equations:
$ \dfrac{\partial J}{\partial A} = \displaystyle \sum_{i=1}^N 2 \left(A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right) ( x_i^2 - y_i^2 ) = 0 $
$ \dfrac{\partial J}{\partial B} = \displaystyle \sum_{i=1}^N 2 \left(A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right) ( x_i y_i ) = 0 $
$ \dfrac{\partial J}{\partial D} = \displaystyle \sum_{i=1}^N 2 \left(A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right) ( x_i ) = 0 $
$ \dfrac{\partial J}{\partial E} = \displaystyle \sum_{i=1}^N 2 \left(A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right) ( y_i ) = 0 $
$ \dfrac{\partial J}{\partial F} = \displaystyle \sum_{i=1}^N 2 \left(A x_i^2 + B x_i y_i + (1 - A) y_i^2 + D x_i + E y_i + F \right) = 0 $
The above are $5$ non-homogeneous linear equations in $A, B, D, E, F$, that can be solved readily for the $5$ unknowns.
We're done.
To obtain the standard parameters of this ellipse, so that you can plot it, follow the steps below.
First, note that
$ A x^2 + B x y + C y^2 + D x + E y + F = 0 $
Can be written as
$r^T Q r + b^T r + F = 0 $
where
$ r = \begin{bmatrix} x \\ y \end{bmatrix} $
$ Q = \begin{bmatrix} A && \dfrac{B}{2} \\ \dfrac{B}{2} && C \end{bmatrix} $
$ b = \begin{bmatrix} D \\ E \end{bmatrix} $
The next step is to find the center of the ellipse, it is given by
$ r_0 = -\dfrac{1}{2} Q^{-1} b = -\dfrac{1}{2} \begin{bmatrix} A && \dfrac{B}{2} \\ \dfrac{B}{2} && C \end{bmatrix}^{-1} \begin{bmatrix} D \\ E \end{bmatrix} $
With this, the ellipse equation becomes
$ (r - r_0)^T Q (r - r_0) = - F + r_0^T Q r_0 $
Define the constant $K = - F + r_0^T Q r_0 $. Divide both sides of the equation by this constant. This will give you
$ (r - r_0)^T Q' (r - r_0) = 1 $
which is the standard algebraic equation of an ellipse.
The next step is to diagonalize $Q'$ by finding its two eigenvalues and the corresponding unit eigenvectors. Then you can write $Q'$ as follows
$ Q' = R D R^T $
where $D $ is the diagonal matrix whose diagonal entries are the two eigenvalues, and matrix $R$ has the two corresponding unit eigenvectors as its columns.
Equation of the ellipse becomes
$ (r - r_0)^T R D R^T (r - r_0) = 1 $
Introduce the new vector $p = D^{(1/2)} R^T (r - r_0) $
Where $D^{(1/2)} $ is the square root of $D$, i.e., it is the diagonal matrix whose diagonal entries are the square roots of the diagonal entries of $D$.
It follows that $r = r_0 + R D^{-(1/2)} p $
Plugging this into the above equation, we get
$ p^T p = 1 $
which means that $ p $ is a unit vector. The standard unit vector in $\mathbb{R}^2 $ is
$ p(t) = \begin{bmatrix} \cos t \\ \sin t \end{bmatrix} $
Therefore, finally, we now have an explicit parametrization of the ellipse, which is
$ r = r_0 + R D^{-(1/2)} p(t) $
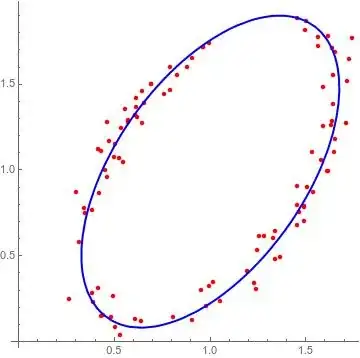
yvalues? They are not linear in x unless A,B,C are small relative to the other params, I think? – Sanjay Manohar Aug 13 '21 at 11:32