Algebraic proof of $\tan x>x$

Question

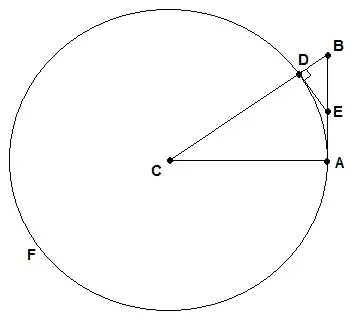
I'm looking for a non-calculus proof of the statement that $\tan x>x$ on $(0,\pi/2)$, meaning "not using derivatives or integrals." (The calculus proof: if $f(x)=\tan x-x$ then $f'(x)=\sec^2 x-1>0$ so $f$ is increasing, and $f(0)=0$.) $\tan x$ is defined to be $\frac{\sin x}{\cos x}$ where these are defined by their infinite series. What I have so far:

$$|z|\le1\implies\left|\sum_{n=4}^\infty\frac{z^n}{n!}\right|<\sum_{n=0}^\infty\frac{|z|^4}{4!\,5^n}=\frac{5|z|^4}{4\cdot 4!}$$ $$\left|\sin x-\Big(x-\frac{x^3}6\Big)\right|=\Im\left[\sum_{n=4}^\infty\frac{(ix)^n}{n!}\right]<\frac{5x^4}{4\cdot 4!}<\frac{x^3}6$$ $$\left|\cos x-\Big(1-\frac{x^2}2\Big)\right|=\Re\left[\sum_{n=4}^\infty\frac{(ix)^n}{n!}\right]<\frac{5x^4}{4\cdot 4!}<\frac{x^2}6$$

Thus $\sin x>x-\frac{x^3}3$ and $\cos x<1-\frac{x^2}3$, so $\tan x>x$. However, this only covers the region $x\le1$, and I still need to bound $\tan x$ on $(1,\pi/2)$. My best approximation to $\pi$ is the very crude $2<\pi<4$, derived by combining the above bounds with the double angle formulas (note that $\pi$ is defined as the smallest positive root of $\sin x$), so I can't quite finish the proof with a bound like $\sin x>1/\sqrt 2$, $\cos x\le\pi/2-x$ (assuming now $x\ge1\ge\pi/4$) because the bound is too tight. Any ideas?

Answer 1

Here is a not-so-original geometric proof.

In unit circle $F$, draw $\Delta ABC$ with $C$ at the center of $F$ and $\overline{AB}$ tangent to $F$ at $A$. Let $D$ be a point on $\overline{BC}$ and $E$ be a point on $\overline{AB}$ such that $\overline{DE}$ is tangent to $F$ at $D$. Furthermore, let $\theta=\measuredangle ACB$.

It is clear that $\tan\theta = \lvert\overline{AB}\rvert$ because $\measuredangle CAB = \pi/2$ due to tangency. As well, $\tan\theta=\lvert\overline{AE}\rvert+\lvert\overline{EB}\rvert$, but $\lvert\overline{ED}\rvert\lt\lvert\overline{EB}\rvert$ because $\lvert\overline{EB}\rvert$ is the hypotenuse of $\Delta BDE$. Thus we have $$\tan\theta\gt\lvert\overline{ED}\rvert+\lvert\overline{EA}\rvert$$ From the diagram we see that sector ACD $\subset$ quadrilateral ACDE, and because both are convex sets, the perimeter of sector ACD $\lt$ perimeter ACDE or $$\lvert\overline{AC}\rvert+\lvert\overline{CD}\rvert+\lvert arc\:DA \rvert \lt \lvert\overline{AC}\rvert+\lvert\overline{CD}\rvert + \lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert$$ $$\lvert arc\:DA \rvert \lt \lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert$$ Finally we have $$\theta=\lvert arc\:DA \rvert \lt \lvert\overline{DE}\rvert+\lvert\overline{EA}\rvert\lt\lvert\overline{EA}\rvert+\lvert\overline{EB}\rvert=\tan\theta$$

Answer 2

Here is a sketch of what you might be looking for:

Showing $\tan x > x$ is equivalent to showing $\sin x - x \cos x > 0$, since $\cos x > 0$ on $(0,\pi/2$).

The series for $\sin x - x \cos x$ is $\displaystyle\sum_{j=1}^{\infty} \dfrac{(2j)x^{2j+1}}{(2j+1)!} = x^3/3 - x^5/30 + x^7/840 - x^9/45360 \ldots$

Group the terms in pairs: $(x^3/3 - x^5/30) + (x^7/840 - x^9/45360) + \ldots$. If $0 < x < \sqrt{10}$, the first difference is positive. The ratio of the terms in each difference is decreasing, so if the first difference is positive, all the rest are too, and the sum is positive. So $\sin x - x \cos x > 0$ on $0 < x < \sqrt{10}$, which gives you quite a bit of leeway since $\sqrt{10} > \pi/2$. (The first positive solution to $\sin x - x \cos x = 0$ happens at $x \approx 4.493$ according to WolframAlpha.)

Answer 3

I'm adding a second answer because the method is very different.

This proof uses the double angle formulas for sine and cosine. From

$$\sin 2x=2\sin x\cos x\qquad\cos2x=2\cos^2x-1$$

we get

$$\tan2x=\frac{\sin2x}{\cos2x}=\frac{2\sin x\cos x}{2\cos^2x-1}>\frac{2x(1-x^2/3)(1-2x^2/3)}{2(1-x^2/3)^2-1},$$

using the bounds $\sin x>x(1-x^2/3)$, $1-2x^2/3<\cos x<1-x^2/3$ derived in the original post. Letting $y=x^2/3$, we have:

\begin{align}\frac{2x(1-y)(1-2y)}{2(1-y)^2-1}>2x&\iff(1-y)(1-2y)>2(1-y)^2-1\\ &\iff1-3y+2y^2>1-4y+2y^2\\ &\iff y>0. \end{align}

Now $y=x^2/3>0$ for $x\ne0$, and the first step is justified when $2(1-y)^2-1>0$, but $0<\cos 2x<2(1-x^2/3)^2-1$ ensures that this is the case, so we can conclude $\tan2x>2x$ for all $x\in(0,1]$ such that $\cos 2x>0$, which is to say, when $2x\in(0,\pi/2)$ (since $\pi/4<1$).

PS: This answer has been successfully turned into a formal proof.

Answer 4

(I should have added this as comment but don't have privilege yet)

Just in case OP haven't checked out yet, the infinite series expansion of $tan(x)$ is already available on Wikipedia. Quoting here:

$$tan(x) = x + \frac{1}{3}x^3 + \frac{2}{15}x^5 + \frac{17}{315}x^7 + {...}$$

for $\lvert x \rvert < \frac{\pi}{2}$.

Answer 5

Equivalent to showing that $\arctan t<t$.

But $$ \arctan t=t-\frac{t^3}{3}+\frac{t^5}{5}+\cdots =\int_0^t\frac{ds}{1+s^2}<t, $$ for $t>0$.

Answer 6

The following is an attempt to transform "the calculus proof" into a non-calculus proof by writing out all the definitions directly.

Fix $a\in(0,\pi/2)$ and let $f(x)=\sin x-x\cos x$ and $g(x)=f(x)-xf(a)/a$. We wish to prove that $f(a)>0$. Let $z$ be an interior extremal point of $g(x)$ in $(0,a)$, which must exist because $g(0)=g(a)=0$ and $[0,a]$ is compact (this is the extreme value theorem). Then

$$\frac{g(z+h)-g(z)}h=\frac{f(z+h)-f(z)}h-\frac{f(a)}a\le0$$

for $h>0$ if $z$ is a maximum, or for $h<0$ if $z$ is a minimum. Now the difference quotient is

$$\frac{f(z+h)-f(z)}h=\\ \cos z\Big(\!\frac{\sin h}h-\cos h\Big)+(\sin z-z\cos z)\frac{1-\cos h}h+\sin z\sin h+z\sin z\frac{\sin h}h.$$

The bounds in the original question are sufficient to prove that the limits $\sin h\to0$, $\cos h\to1$, $\frac{\sin h}h\to1$, and $\frac{1-\cos h}h\to0$ exist as $h\to0$, so the above difference quotient tends to the last term, $z\sin z>0$, and in particular there is an $h$ near $0$ such that the above quotient is greater than zero. (This can also be written explicitly by combining the bounds to find a specific value for $h$.) For this $h$,

$$0<a\frac{f(z+h)-f(z)}h\le f(a).$$

Yes, it's thinly veiled calculus, but the proof itself makes no direct mention of derivatives.