Given a region of the complex plane and a map $z \to f(z)$, is there a general way to "naturally interpolate" the point $z$ to $f(z)$ in such a way that the movement follows a "natural" smooth path that doesn't generate unnecessary "kinks" and overlaps?
Background: I make educational animations. A couple of projects I've been playing around with involve complex numbers. I'm trying to figure out a general method to animate complex maps that look good and natural in terms of smooth deformations of the complex plane.
Forgive me, but I have no way to confidently and formally state this question at this point. But I can illustrate it.
Here's a great video illustrating Möbius transformations. You can see that for the inversion, the points on the plane follow a quite natural path from start to finish. This follows naturally from the rotation of the sphere used in the projection, in this particular case.
But here's what a naive linear interpolation ($z \to (1-t) z + t f(z)$, with $0 \leq t \leq 1$) of the same transformation $z \to \frac{1}{z}$ looks like:
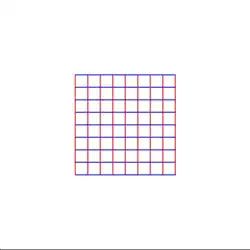
As you can see, this method creates a lot of "kinks" and weird bends along the way. (Also, ignore the straight lines). I'm trying to avoid this, as it makes the animation more confusing than it should be.
Some other examples. Here's the same method for $z \to z^2$:
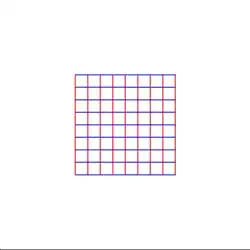
And $z \to e^z$ (using $[-1,1] \times [-\pi,\pi]$):
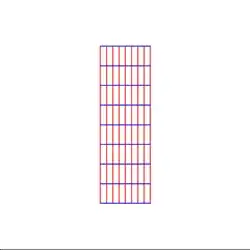
In all these cases, I can imagine different and more natural ways to deform along the way, but I haven't come up with a general way to tackle this problem yet. I'm hoping there's something in complex analysis that can be helpful here, but I haven't found anything yet. Any ideas?
EDIT: Here's $z \to e^z$ using Rahul's method with some translation:
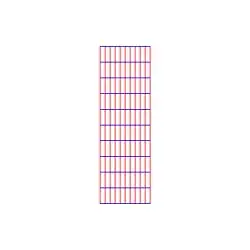
This is pretty much a perfect example of the sort of "natural" transformation I'm looking for. Each new step seems like an obvious deformation of the previous step following the same overall "style". It creates a nice sense of deliberation, which makes the movement intuitive, comprehensible and predictable.

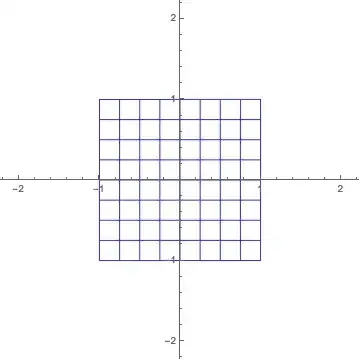
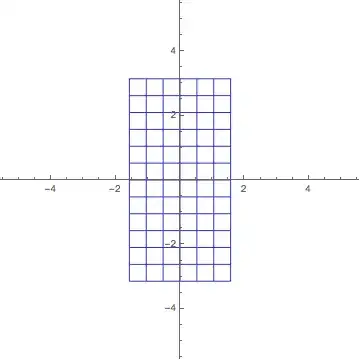


I do mean interpolate in a sense, since what I'm trying to do is move the point $(a,b)$ corresponding to $z = a + bi$, to some point corresponding to $f(z)$. Using $w = (1-t)z + t f(z)$ is the linear interpolation I used above, which is the naive way.
So the sophisticated approach is to change $f(z)$ itself in some clever way, and this is what I'm trying to do. I'm looking for a general and robust method to perform this to arbitrary functions.
– LucasVB Jul 30 '14 at 01:27