I am having some diffucilty sketching the unit ball centered at $(0,0)$ for the metric given by $$d(x,y)=\sum_{i=1}^n \vert x_i -y_i \vert$$ in $\mathbb{R}^n$ for $n=2$. If $n=2,$ the unit ball is the set of all pairs (this already kind of confuses me-it would make more sense to discuss the set of all points instead the set of all pairs of points) $(x_1,y_1),(x_2,y_2)\in\mathbb{R}^2$ for which $$\vert x_1-y_1\vert+\vert x_2-y_2\vert<1\,\,\,\,\,\,\,\,(*)$$
From $(*)$ we obtain four inequalities: $$ \begin{cases} x_1-y_1+x_2-y_2<1, \\ x_1-y_1+y_2-x_2<1, \\ y_1-x_1+x_2-y_2<1, \\ y_1-x_1+y_2-x_2<1 \end{cases} $$
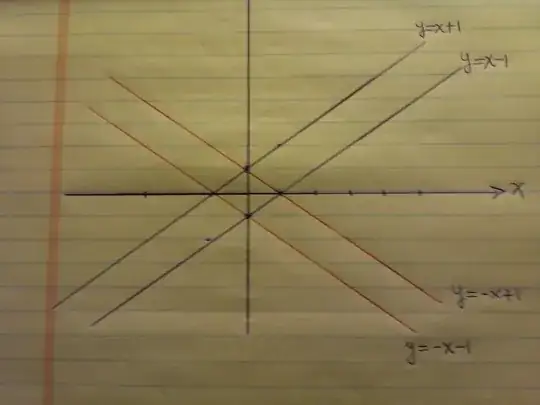
To find the region determined by these inequalities, I attempt to find the boundary of the region by replacing $<$ with $=$ in these inequalities. In the first equality I can set $x_2=y_2=0$ to obtain $x_1-y_1=1$, which is a line with slope 1 and y-intercept at $(0,-1).$ Similarly, I find the lines $y=-x+1,y=-x-1,y=x+1.$ If I had to guess, the ball would be the set of points strictly between the red lines or the blue lines in the picture below. However, I believe this is a very crude estimate to the boundary of my ball because I set $x_2=y_2=0$ the entire time; in some sense I crudely eliminated one of my parameters. Am I correct, and is there a more rigorous way to find the ball (or its boundary)?