My data is not normally distributed: what can I do to estimate a tail probability?

Question

Continuing on from my earlier question, I'm attempting to analyse the data qualitatively.

In the following plot, I make $10000$ samples where I count "the number of clashes". I plot $n$ vs. the number of times $n$ clashes occurred.

(The number of clashes is a measure of "how wrong" an attempted attack was [on the secret sharing scheme I'm looking at]).

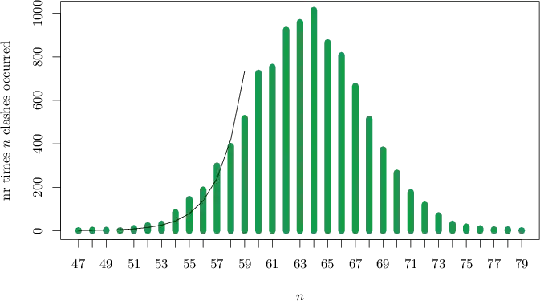
(Drawn using tikzDevice for R, then edited manually.)

In R, it fails the shapiro.test, so it's not normally distributed:

> shapiro.test(z[1:5000])

    Shapiro-Wilk normality test

data:  z[1:5000]
W = 0.9947, p-value = 1.597e-12

So:

Q: How can I estimate the probability $p$ of $0$ clashes from the above distribution?

It should be very small, around $10^{-14}$:

• I have a theoretical lower bound of $1.046 \times 10^{-14}$, and I expect it to be close to the actual value.
• I have made $10^{11}$ samples, and all had at least one clash.

I attempted to fit an exponential curve to the left hand side (drawn above): the curve is $$3.29 \times 10^{-12} \exp(0.56n)$$ which, when $n=0$ gives the estimate $\hat{p}=3.29 \times 10^{-16}$. But I know that this estimate is off by around a factor of $100$, which makes me think this is not the best approach. (Or maybe I should fit some other curve, or use more samples. Or maybe this level of confidence is to be expected.)

---

Addendum:

• I'm trying to show that $\mathrm{Pr}[0 \text{ clashes}]$ is small (say less than $10^{-8}$ or $10^{-9}$). So the estimate doesn't need to be precise, but I need to have confidence in the estimate.

• The theoretical maximum number of clashes is $220$ (this number can be achieved).

• "Do you know the statistical power of the Shapiro-Wilk test for such a large sample size?" In short, no, I don't. But we can compare the results to random data from a normal distribution:

  > shapiro.test(rnorm(5000, mean = mean(z), sd = sd(z)))
  
      Shapiro-Wilk normality test
  
  data:  rnorm(5000, mean = mean(z), sd = sd(z))
  W = 0.9996, p-value = 0.4053
  

  While the results fluctuate between runs, they don't seem comparable to my data.

  I also tried with fewer samples included and it didn't seem to "help".

  > shapiro.test(z[1:100])
  
      Shapiro-Wilk normality test
  
  data:  z[1:100]
  W = 0.9757, p-value = 0.06116
  

  compared to

  > shapiro.test(rnorm(100, mean = mean(z), sd = sd(z)))
  
      Shapiro-Wilk normality test
  
  data:  rnorm(100, mean = mean(z), sd = sd(z))
  W = 0.9845, p-value = 0.2932
  

  (Here, it fluctuates quite a lot.)

• I'm capable of making around $10^{10}$ samples, if it would help.

Answer 1

Let $C=$ Number of Clashes and $p_0 = P(C=0)$. In general, your distribution is a discrete probability mass function. However, since you only care about a single value $(C=0)$ the rest of the distribution is somewhat irrelevant.

Therefore, one simple approach is to develop a conservative confidence interval for $p_0$ by inverting the hypothesis test for a binomial proportion:

$H_0: p_0=p\;\;\text{vs.}\;\; H_a: p_0<p$

There are two common (approximate) approaches to constructing binomial proportion CIs : The normal approximation and the Wilson Score Interval. Unfortunately, since we expect $p_0 \ll .001$, these approximate intervals will likely not have the desired true confidence level.

Instead, I would recommend using a Clopper-Pearson confidence interval. Not only is it based on the exact binomial distribution, but it is guaranteed to achieve its nominal confidence level (as opposed to only approximately for the other two). In fact, it is usually quite conservative, in that a 95% CI may actually achieve a 99% coverage probability, but it will not be less than 95%. For "typical" values of p, (e.g., between .01 and .99) the approximate intervals are generally preferred because they are usually close to their nominal coverage, while the Clopper-Pearson interval is too conservative. However, this is not your situation, so the Clopper-Pearson is a safer interval for bounding purposes.

Now, with $10^{11}$ data points where each has at least one clash, your CI will be quite easy to construct, and rather close to 0, as you expected. Below is the $1-\alpha$ one-sided Clopper-Pearson CI for $p_0$: (Note that the LB=$1.046 \times 10^{-14}$, as per your theoretical calculation), assuming you have observed an uninterrupted string of N non-zero results.

Upper Bound = $\{p:(1-p)^{N}= \alpha\}=\{p:N\ln(1-p)= \ln(\alpha)\} \rightarrow p=1-\exp(\frac{\ln(\alpha)}{N})$.

Now, with $N=10^{11}$ you will have numerical issues for the usual values of $\alpha =\{.05,.01\}$However, since you indicated that you wanted to know if it is less than, say, $10^{-8}$, we can reverse this process and find the level of confidence with which we can say that $p_0\leq 10^{-8}$:

$10^{-8} = 1-\exp(\frac{\ln(\alpha)}{10^{11}}) \rightarrow \frac{\ln(\alpha)}{10^{11}} = \ln(1-10^{-8}) \rightarrow \alpha = (1-10^{-8})^{10^{11}}\ll 10^{-10}$. Therefore, you can be virtually certain that $p_0<10^{-8}$

If you need actual numbers, I went onto WolframAlpha and got the following values for quantities that you may be interested in:

Confidence level for $p_0<10^{-8}$ = $1-5 \times 10^{-435} \approx 1$

99% one sided CI $\approx 4.6 \times 10^{-11}$

95% one sided CI $\approx 3\times 10^{-11}$

Confidence level for $p_0 < 10^{-13}$ $\approx 0.01$

The last result may be somewhat disappointing, in that we can only bound $p_0$ within 3 orders of magnitude of the theoretical minimum with any reasonable degree of confidence, even with your enormous sample size. Such is the difficulty of extremely small probabilities.

Hope this helps.