Assume the following:
$f_n$ is a sequence of $C^1$ functions on $[0,1]$
$f_n(x) \rightarrow 0$ pointwise.
$f'_n(x) \rightarrow g(x)$ pointwise.
Is it true that $g(x) = 0$ almost everywhere? I think the answer is no, but I'm having trouble with finding a counter-example.
One can show that $\{g=0\}$ is dense:
Suppose $X=\{x\in[0,1]\ :\ g(x)\neq0\}$ has non empty interior.
For $\varepsilon >0$, let $X_n^\varepsilon=\{x\in[0,1]\ :\ f'_m(x)\geq \varepsilon\ \forall m>n\}$, and for $\varepsilon <0$ let $X_n^\varepsilon=\{x\in[0,1]\ :\ f'_m(x)\leq \varepsilon\ \forall m>n\}$
$X_n^\varepsilon$ is closed. Moreover $X\subset \bigcup_{m\in\mathbb Z, m\neq0}\bigcup_nX_n^{1/m}$.
So $\bigcup_m\bigcup_nX_n^{1/m}$ has nonempty interior. As any countable union of closed sets with empty interior has empty interior, there is $\varepsilon$ and $n$ such that $X_n^{\varepsilon}$ has nonempty interior. W.l.g. we can suppose $\varepsilon >0$.
Let $(x,y)$ be an interval contained in $X_n^{\varepsilon}$
We have $$\varepsilon(x-y)=\int_x^y\varepsilon\geq\int_x^yf'_n(x)=f_n(x)-f_n(y)\to 0$$ contradiction.
REMARK: if $f_n'$ where bounded or dominated by an integrable function, then the Lebesgue theorem of dominated convergence applies and we can put the limit inside the integral, so for any $x,y\in[0,1]$ we would have $0=\lim_n(\int_x^yf'_n(t))=\int_x^y\lim_n f'_n(t)=\int_x^yg(t)$ which implies $g=0$ almost everywhere.
COUNTEREXAMPLE:
Here I describe a general conter example via the cantor set construction. The procedure is complicated to describe. I'll describe only the first three steps, hoping that it is clear how to continue. (If one could use the standard cantor set, the construction would be nicer, but the cantor set has zero measure!)
Let's consctruct a cantor-set-like set $X$. We remove from $[0,1]$ a central interval $(a_1,b_1)$, of size $\delta_1$. Then we remove two intervals $(a^0_2,b^0_2)$, central in $[0,a_1]$ and $(a^1_2,b^1_2)$ central in $[b_1,1]$, both of the same size $\delta_2$. We go on like in the construction of the cantor set. We choose the sizes $\delta_i$ so that the total measure of the remove parts in the proces is $1/2$, so that the remaining set $X$ will have measure $1/2$.
We describe now the functions $g_n=f'_n$ and define $f_n(x)=\int_0^xg_n(t)$.
The functions $g_n$ will be piecewise linear.
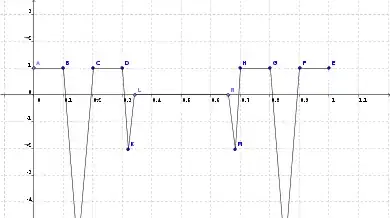
CONSTRUCTION of $g_1$. (see also the picture below)
$g_1(x)=1$ for $x\in[0,a_1]$. Then in $[a_1,1/2]$ define $g_1$ so that it is linear and $\int_0^{1/2} g_1(t)=0$. Finally, on $[1/2,1]$ defines $g_1$ symmetrically by imposing $g_1(x)=g_1(1-x)$.
CONSTRUCTION of $g_2$. (see also the picture below)
We modify $g_1$ as follows:
On $[0,a_1]$ we define $g_2$ so that $g_2(x)=1$ for $x\in[0,a^0_2]$ and $[b^0_2,a_1]$. On $[a^0_2,b^0_2]$ extends $g_2$ so that $\int_0^{a_1}g_2(t)=0$.
On $[a_1,1/2]$ we set $g_2(a_1)=1$, $g_2(a_1+\epsilon_2)=0$ and we extentd by a piecewise linear function so that $\int_{a_1}^{a_1+\epsilon_2}g_2(t)=0$ and so that $|g_2(t)|<10\epsilon_2$ on $[a_1,a_1+\epsilon_2]$
Finally, on $[1/2,1]$ we define $g_2$ symmetrically by imposing $g_2(x)=g_2(1-x)$.
Note that
1) $f_1=\int g_1$ is bounded by $(1-\delta_1)/2$, $\int_0^1 f_1=0$.
2) $f_2=\int g_2$ is bounded by $(\frac{1-\delta_1}{2}-\delta_2)/2<1/4$ on $[0,a^0_2],[b^0_2,a_1],[b_1,a_2^1]$, and $[b_2^1,1]$; $\int_0^{a_1}g_2=\int_0^1f_2=0$ and $f_2=0$ on $[a_1+\epsilon_2,b_1-\epsilon_2]$, and on $[a_1,a_1+\epsilon_2]$ is bounded by a constant dependint on $\epsilon_2$.
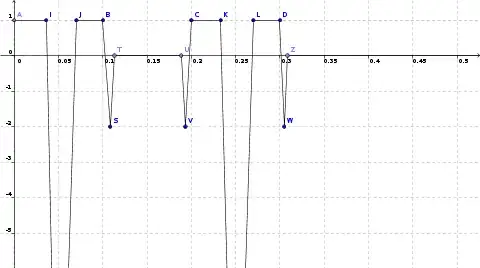
CONSTRUCTION OF $g_3$
On $[a_1,b_1]$ we just change $\epsilon_2$ with a smaller $\epsilon_3$
On the other intervals we do the same changes we did for passing from $g_1$ to $g_2$.
This construction leads to $f_n$ which is uniformly bounded by $(1/2)^2$ and a constant depending on $\epsilon_n$, which goes to zero.
on $X$, which is the complement of the removed intervals $g_n=1$ for al $n$. On the intervals removed $g_n(x)\to 0$ because we choose $\epsilon_n\to 0$.
In particular $g_n$ has a point wise limit which is the characteristic fucntion of $X$. None theless $g_n$ is not uniformly bounded because each $g_n$ has pieces where it is extremely negative (such pieces are tamed at time $n+1$) due to the fact that we require $\int g_n=0$ on intervals $[0,a_n^i]$.
Here some very rude graphics of $g_1$, $g_2$, and $g_3$ (note that the third picture is the graphic of $g_3$ zoomed at the interval $[0,1/2]$, so it is "half" of $g_3$)
