9

If a point on a 2D lattice is allowed to take a random walk by taking a unit step either up, down, left or right, there is probability $1$ of reaching any point (including the starting point) as the number of steps approaches infinity.

enter image description here

However, if further limiting rules are added, the probability of the point reaching distance $d$ from the startpoint is altered.

What is the expected distance $d$ from the startpoint given the following rules:

1) The point may not "go back on itself" (eg, if move #3 is up, move #4 cannot be down)

2) The random walk finishes if the point "crashes into" any previous path it has taken (ie, it cannot take a path it has taken previously)?

(Clearly the minimum number of steps is 4.)

martin
  • 9,168
  • This problem is hard because you cannot use the Markov property. Did you try a simulation? – Lost1 Jul 04 '14 at 12:32
  • Not yet - no access to a computer at the moment – martin Jul 04 '14 at 12:44
  • But you can meet a vertex twice? – draks ... Jul 04 '14 at 12:51
  • 2
    How do you count the distance for the walks that already crashed? – Did Jul 04 '14 at 13:02
  • @ Draks, yes that is ok - no crash there – martin Jul 04 '14 at 13:34
  • @Did - as the crow flies from the startpoint – martin Jul 04 '14 at 13:35
  • This is not my question: at time N, many walks are already stopped, do you count them to compute the expected distance from the startpoint? – Did Jul 04 '14 at 13:49
  • And the number of steps still goes to infinity? – draks ... Jul 04 '14 at 13:58
  • @ Did, I don't really understand. If one walk crashes, that is the end of that walk (it may be only 5 steps, for example). The distance from the start-point would in that case, be 0. My question is, what is the expected distance before crash for $n$ walks as $n$ approaches infinity? – martin Jul 04 '14 at 14:37
  • @ Draks - yes (see above comment to Did) – martin Jul 04 '14 at 14:38
  • "The distance from the start-point would in that case, be 0." ?? This is still difficult to understand, so let me try again. After $n$ steps, $k$ walks already crashed and $4^n-k$ did not yet (say they are still alive). Let $(c_i){i\leqslant k}$ denote the distances between the crash points of those who crashed and the origin. Let $(a_j){j\leqslant 4^n-k}$ denote the distances between the endpoints of the walks still alive and the origin. Please write the quantity of interest in terms of $(c_i)_i$, $(a_j)_j$, $k$ and $n$. – Did Jul 24 '14 at 13:07
  • (Unrelated: Adding a space between @ and user is a sure way that user does not get notified.) – Did Jul 24 '14 at 13:07
  • This looks like a self-avoiding random walk. Hard problem. Maybe somehting like this (or references inside) will help: http://math.bme.hu/~vetob/publ/htv3/htv_ptrf.pdf – rrv Apr 16 '20 at 11:36

1 Answers1

1

Rule 1 doesn't affect the process much:

Given a standard random walk of the form you initially describe, recursively removing backtracks (e.g. the subsequence ULRRLD would get removed) yields a walk following rule 1, and importantly, does not introduce any bias into the process (i.e. the three available options (under rule 1) are equally likely also in this "standard random walk with backtracks removed" process.

It does affect the time taken, speeding up the process by a surprising factor of 3. This is because every non-backtracking step taken in the standard process has an equal chance $p$ of being undone due to later backtracking, which is $p = 1/(1+3(1-p)) = 1/(4-3p)$, so $3p^2-4p+1=0$, and we get $p=1/3$. (The solution $p=1$ is not an attracting point of the original recursion.) So 1/3 of the steps will be annulled due to backtracking by another 1/3 of the steps, leaving only the remaining 1/3 in the reduced path that follows rule 1.

It also affects the set of "already taken" points and segments, which will affect the "time to crash".

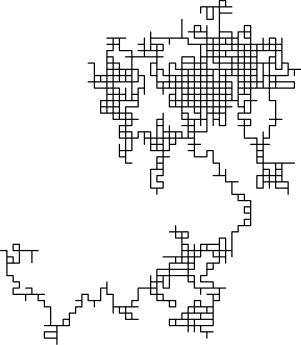
Rule 2 has a big effect on the process, and since it involves remembering the entire path history, it belongs to a class of questions that generally do not have closed-form solutions.

However, we can still get a strong bound on the expected distance, because it cannot exceed the expected running time. Even just considering crashes due to going around a square (three consecutive right turns, or three consecutive left turns), we can get a bound (using a method like this) on the expected survival time of less than 20, and thus the expected distance when it crashes will be much less than 20.

Community
  • 1
Matt
  • 9,693