Draw three congruent circles all touching one another, and a second set of three such circles, each touching also two of the first set.

Question

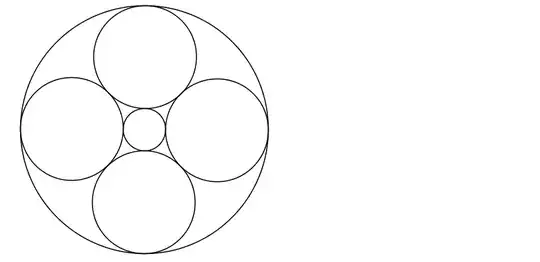
This corresponds to a Steiner's Porism configuration with n = 4, however the trouble I'm having is that while it is easy to construct an n = 4 Steiner's Porism configuration (see second image below), I don't know what the circle of inversion would be that would invert it into the desired instantiation.

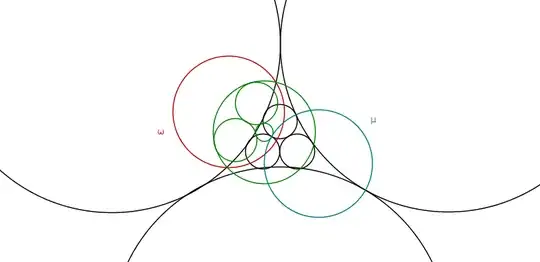
I was able to do some eyeballing (together with some observations such as that the outer 3 circles must be centered on the radical axes of pairs of the inner circles), using the excellent geometry software C.a.R. to snap to intersections, to construct an approximate diagram below, from which I was also able (approximately) to construct the circle of inversion $\omega$ (shown in red).

In black is shown the configuration as described, while in green are shown 4 of the 'regular 4-gon' figure resulting from inversion in $\omega$ (inner and outer concentric circles and two of the four congruent circles).

While the fact that this inversion works (again, approximately) shows that my eyeballing construction is reasonably close, I still would not know how to precisely construct $\omega$ directly from the regular 4-gon version of the n=4 configuration.

Also shown in light blue is a mid circle $\mu$ between two of the opposite circles in black of the described configuration.

This is problem 5.8.3 in Geometry Revisited (by Coxeter and Greitzer).

Answer 1

A construction for the original problem can be derived from the following observation:

Let us denote the touching smaller circles C1, C2, C3 with centers M1, M2, M3, resp., each with radius r. Let C4 be one of the bigger circles C4 touching C1 and C2 with (unknown) radius R and let C4´ be a circle with radius (R+r) and same center. This is a circle going through M1 and M2 and it touches a line g parallel to the symmetrie axis s1 between M2 and M3 with a distance of r between g and s1 (into the obvious direction).

To construct the circle C4´ through given points M1 and M2 and with given tangent g we perform an inversion at circle C with center M1 and radius |M1M2|. C4´ is thus mapped to a line running through M2 and touching the circle which is the image of g (after inversion).

So the construction of C4 (having constructed C1,C2,C3 already) runs as follows:

1. draw g as a line parallel to the symmetry axis s1 with distance r from s1 on the side of M3.
2. invert g at circle C giving a circle Cg.
3. draw the tangents from M2 to Cg.
4. invert the tangents and choose the bigger circle as C4´ and its radius (R+r).
5. reduce this radius by r to get R. C4 is the circle with the same center as C4´ and radius R.
6. Circles C5 and C6 are easily constructed using the symmetry axes, the symmetry center and the now known radius R.

Answer 2

Here is an analytical solution for finding the appropriate inversion center:

Let $R$ be the radius of the four congruent circles in Steiner's Porism configuration with n = 4. (Then the small circle in the center has radius R($\sqrt2 -1)$ while the outer circle has radius $R(\sqrt2+1)$.)

We are looking for a center of inversion along a line through the center of the Porism configuration which is also a tangent to each of the 4 congruent circles (i.e. the line is inclined to the horizontal by 45° in the above figure). Because of symmetry such an inversion will generate two pairs of congruent circles from the 4 congruent circles. If the center circle is transformed to a circle congruent to one of the pairs, the outer circle will be transformed to a circle congruent to the other pair.

Let $x$ be the distance of the inversion center from the configuration center. Then the distance of the inversion center to 4 congruent circles' center will be $\sqrt{(x\pm R)^2+R^2}$. The radius of a circle at distance $d$ from the inversion center (with a unit inversion circle) is transformed from $r$ to $\frac{r}{d^2-r^2}$ by inversion. Hence the radii of the 4 congruent circles will be transformed to $\frac{R}{(x\pm R)^2}$. The radius of the center circle will be $\frac{R(\sqrt2-1)}{x^2-R^2(\sqrt2-1)^2}$ after the inversion.

To make the inverted center circle congruent to one pair of already congruent circles we solve

$\frac{R}{(x + R)^2} = \frac{R(\sqrt2-1)}{x^2-R^2(\sqrt2-1)^2}$

for $x$, which gives the two valid solutions $R\frac{1\pm \sqrt3}{\sqrt2}$. Such a distance can, of course, now also be constructed.