CONSTRUCTION :
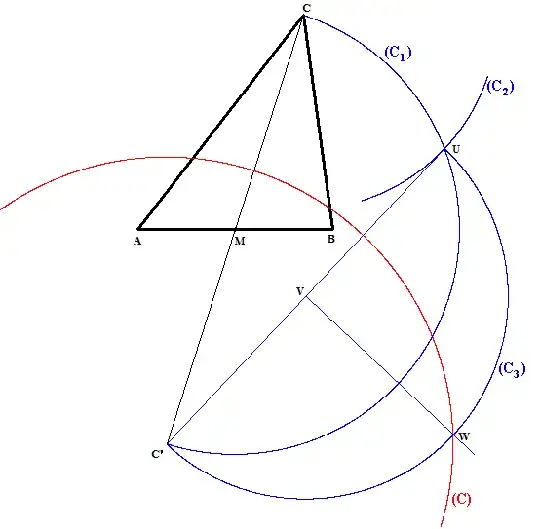
Given the triangle ABC: M is the middle of AB. C' is symmetric of C relatively to M.
Draw the semi-circle $(C_1)$ of diameter CC'.
Draw an arc of circle $(C_2)$ of center C and radius=$\overline{AB}$.
$(C_1)$ and $(C_2)$ intersect in U.
Draw the semi-circle $(C_3)$ of diameter C'U.
V is the middle of C'U. From V, draw a straight line orthogonal to C'U. It intersects $(C_3)$ in W.
Draw the circle $\color{red}{(C)}$ of center C' and radius=$\overline{C'W}$
From right triangle CUC' :$\quad\overline{C'U}^2=\overline{C'C}^2-\overline{AB}^2$
From right triangle C'WU :$\quad 2\overline{C'W}^2=\overline{C'U}^2$
$$\overline{C'W}^2=\frac{1}{2}\left(\overline{C'C}^2-\overline{AB}^2 \right)$$
$$\overline{C'W}^2=2\left(\overline{C'M}^2-\overline{MB}^2 \right) \tag 1$$
We will show that the circle $\color{red}{(C)}$ of center C' and radius=$\overline{C'W}$ is the locus of the points P such that
$$\overline{PA}^2+\overline{PB}^2=\overline{PC}^2$$
PROOF :
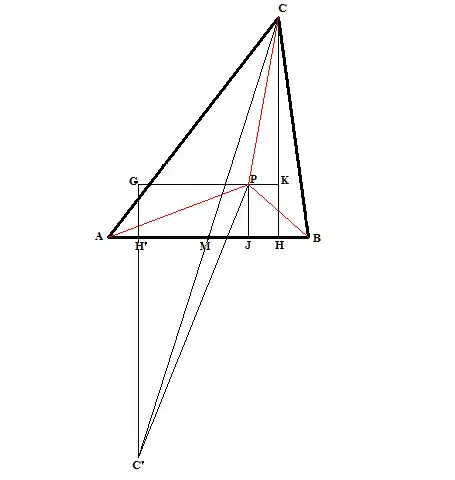
H is the orthogonal projection of C on AB. H' is symmetric of H relatively to M.
First, consider an arbitrary point P , not necessarily on $\color{red}{(C)}$
J, K, G are the orthogonal projections of P respectively on AB, CH, C'H' (or on straight extension).
The Pythagorean theorem in the respective right triangles gives :
$\overline{PA}^2=(\overline{AM}+\overline{MJ})^2+\overline{JP}^2$
$\overline{PB}^2=(\overline{MB}-\overline{JB})^2+\overline{JP}^2$
$\overline{PC}^2=\overline{PK}^2+\overline{KC}^2=(\overline{MH}-\overline{MJ})^2+(\overline{HC}-\overline{JP})^2 $
Second, consider a particular point P with condition :
$$\overline{PA}^2+\overline{PB}^2=\overline{PC}^2$$
$(\overline{AM}+\overline{MJ})^2+\overline{JP}^2+(\overline{MB}-\overline{MJ})^2+\overline{JP}^2=(\overline{MH}-\overline{MJ})^2+(\overline{HC}-\overline{JP})^2$
After expending and few transformations :
$(\overline{MH}+\overline{MJ})^2+(\overline{HC}+\overline{JP} )^2=2\overline{MH}^2+2\overline{HC}^2-\overline{AM}^2-\overline{MB}^2$
$$(\overline{MH}+\overline{MJ})^2+(\overline{HC}+\overline{JP} )^2=2\overline{MH}^2+2\overline{HC}^2-2\overline{MB}^2$$
$\overline{MH}+\overline{MJ}=\overline{H'M}+\overline{MJ}=\overline{H'J}=\overline{GP}$ and
$\overline{HC}+\overline{JP}=\overline{C'H'}+\overline{H'G}=\overline{C'G}$
$$\overline{GP}^2+\overline{C'G}^2=2\overline{MH}^2+2\overline{HC}^2-2\overline{AB}^2$$
In the right triangle C'GP : $\overline{GP}^2+\overline{C'G}^2= \overline{C'P}^2$
$$\overline{C'P}^2=2\overline{MH}^2+2\overline{HC}^2-2\overline{MB}^2$$
$$\overline{C'P}^2= 2\overline{MC}^2-2\overline{MB}^2 = 2\overline{C'M}^2-2\overline{MB}^2$$
A, B, C, H, M are fixed points. Hence $\quad 2\overline{C'M}^2-2\overline{MB}^2$ = Constant.
$\overline{C'P}$ is of constant lengh. Thus the point P is on a circle of center C' and radius $R$. This is the locus.
$$R^2=2\overline{C'M}^2-2\overline{MB}^2$$
Compare this result to the previous (1) above :
$\quad\overline{C'W}^2=2\left(\overline{C'M}^2-\overline{MB}^2 \right)$
Indeed, circle $\color{red}{(C)}$ defined on the first figure is the locus.

