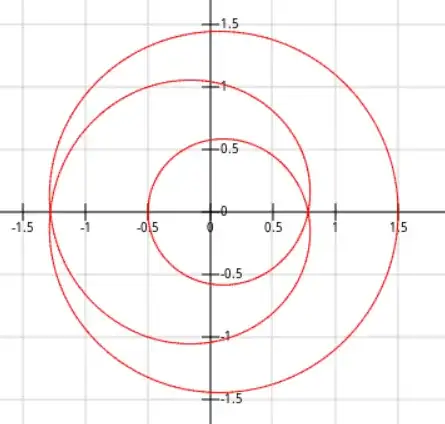
Let $f(z)=z^3+\frac{z^2}{2}$. Let $D$ be the unit disk in $\mathbb{C}$. How to compute $$ Area(f(D))? $$
In the case that $f:D\to \mathbb{C}$ is injective, \begin{align*} Area(f(D))&= \int_D |f'(z)|^2 ~ dx\,dy \\ &= \int_0^1 \int_0^{2\pi} r\left|f'(re^{i\theta})\right|^2 ~ d\theta \, dr \\ &= \int_0^1 \int_0^{2\pi} r \left(\sum_{n = 1}^\infty nc_nr^{n-1} e^{i(n-1)\theta}\right)\left(\sum_{n = 1}^\infty n\overline{c_n}r^{n-1} e^{-i(n-1)\theta}\right) ~ d\theta \, dr \\ &= \int_0^1\left( \sum_{n=1}^\infty 2\pi n^2|c_n|^2 r^{2n-1} \right)~dr \\ &= \sum_{n=1}^\infty \frac{2\pi n^2}{2n} |c_n|^2 \\ &= \pi \sum_{n=1}^\infty n|c_n|^2. \end{align*} But now $f$ is not injective. How to compute? Thanks.