Can Nash Equilibrium be more than two?

Question

In the Prisoner's Dilemma example, we know that there is only one Nash Equilibrium.

That is both of them confess.

Is it possible that there are two Nash equilibriums in one example?

Can you roughly give me such an example?

Answer 1

Yes! In the Nash equilibrium none of the players gains more by deviating his/her strategy from the equilibrium point. For an example in the following two-player reward table, there exist "many" equilibria:

$$\left[ \begin{array}{ccc} 1/1 & 0/0 & 0/0& 0/0& 0/0& 0/0 \\ 0/0& 0/0 & 0/0& 0/0& 0/0& 0/0 \\ 0/0 & 0/0 & 0/0& 0/0& 0/0& 0/0 \\ 0/0 & 0/0& 0/0&1/1 & 0/0& 0/0 \\ 0/0 & 0/0 & 0/0& 0/0& 0/0& 0/0 \\ 0/0 & 0/0& 0/0& 0/0& 0/0 &1/1 \end{array} \right]$$

Answer 2

Most games have an odd number of Nash equilibrium. For example in the coordination game below: $$ \begin{array}{|c|c|c|} \hline P1\backslash P2 & PC & MAC \\ \hline PC & 2,2 & 0,0 \\ \hline MAC & 0,0 & 3,3 \\ \hline \end{array} $$ You have 3 Nash equilibria: (PC,PC), (MAC,MAC) and also one in mixed strategies where each player chooses PC with probability 3/5 and MAC with prob. 2/5.

Answer 3

A bit late to the party here, but you can indeed have two Nash equilibria.

$$ \begin{array}{|c|c|c|} \hline & L & R \\ \hline T & 1,1 & 0,0 \\ \hline B & 0,0 & 0,0 \\ \hline \end{array} $$

Here there are precisely two (pure) equilibria, even if one allows for mixed strategies: $\{T,L\}$ and $\{B,R\}$.

A bit more in-depth, for a 'generic' finite strategic-form game (for our purposes, generic = games without ties in payoffs), you will always have a finite, odd number of equilibria. In fact, when you have weirdness like an even number of equilibria, it usually means one is not 'stable' in some sense. Here, $\{B,R\}$ is the 'theologian's equilibrium': if you're playing it, you best have total faith your opponent is playing along as well. If you have any doubt, then there's a better alternative.

Depending upon your background/interest level, another way of explaining the weirdness of the above example is to note that $\{T,L\}$ trembling hand perfect, while $\{B,R\}$ is not.

Answer 4

Consider 3 hunters, Bob, Charlie, and Doug

with the following choices of things to hunt:

A moose: worth 9 units of food A wolf: worth 4 units of food A rabbit: worth 1.5 units

Now there are plenty of rabbits so if a hunter opts to hunt a rabbit they will definitely get their one rabbit

A wolf requires at least 2 hunters, if 2 hunters hunt it each then each gets 2 units of food, but if all 3 hunters go for the wolf then the pay off is is only 1.3333 units of food so it is more advantangeous to go for an individual rabbit,

Lastly we Moose requires all 3 hunters to be hunted successfully, naturally if hunted each hunter gets 3 units of food resulting in the highest payoof but highest risk.

If we set up our 3 dimensional payoff matrix by presenting its slices

Assume Bob hunts a rabbit (Bob = first index, Charlie = second index, Doug = third index) $$ \left( \begin{array}{ccc} & R & W & M \\ R & 1.5,1.5,1.5 & 1.5,0,1.5 & 1.5,0,1.5 \\ W & 1.5,1.5,0 & 1.5,2,2 & 1.5,0,0 \\ M & 1.5,1.5,0 & 1.5,0,0 & 1.5,0,0 \end{array} \right)\ $$

Assume Bob hunts a wolf

$$ \left( \begin{array}{ccc} & R & W & M \\ R & 0,1.5,1.5 & 2,2,1.5 & 0,0,1.5 \\ W & 2,1.5,2 & 1.33,1.33,1.33 & 2,2,0 \\ M & 0,1.5,0 & 2,2,0 & 0,0,0 \end{array} \right)\ $$

Assume Bob hunts a moose

$$ \left( \begin{array}{ccc} & R & W & M \\ R & 0,1.5,1.5 & 0,0,1.5 & 0,0,1.5 \\ W & 0,1.5,0 & 0,2,2 & 0,0,0 \\ M & 0,0,0 & 0,0,0 & 3,3,3 \end{array} \right)\ $$

Now there are 3 equillibrium strategies for the players:

1. Nobody trusts anybody so they all go rabbit

2. Someone expects at least one person but not the other to be trustworthy so they go the way of wolf

3. Total trust results in the moose

Now if Bob, Charlie, and Doug take random strategies the expected payout for Bob g(and expected payout for Charlie and Doug too by symmetry is)

$$ 1.5 \frac{9}{27} + 2 \frac{4}{27} + \frac{4}{3} \frac{1}{27} + 3 \frac{1}{27} = 0.95...$$

Answer 5

Allowing mixed strategies (u,v), in three dimensions, a smooth regular parameterized manifold of outcomes X = (x(u,v), y(u,v), z(u,v)) all of which are Nash equilibria may form a minimal surface if one is interested in minimizing tension between players, or what is the same, may form a vanishing mean curvature flow of play.

Answer 6

In general, there can be an exponential number of Nash equilibria in a non-degenerate game. For a simple example:

If both players payoff matrices are the $n \times n$ identity matrix then the game has $2^{n}-1$ Nash equilibria. All these Nash equilibria are symmetric and correspond to all non-empty subsets of the set of pure strategies $\{1,\ldots,n\}$. In every equilibrium both players mix uniformly over the same non-empty subset of $\{1,\ldots,n\}$.

So for $n=3$, the game is:

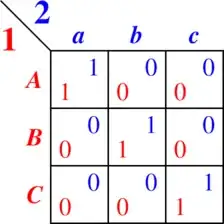
There are $2^3-1=7$ equilibria as follows (EP stands for expected payoff):

1 P1: (1) 1/3 1/3 1/3 EP= 1/3 P2: (1) 1/3 1/3 1/3 EP= 1/3 
2 P1: (2)   0 1/2 1/2 EP= 1/2 P2: (2)   0 1/2 1/2 EP= 1/2 
3 P1: (3) 1/2   0 1/2 EP= 1/2 P2: (3) 1/2   0 1/2 EP= 1/2 
4 P1: (4)   0   0   1 EP=   1 P2: (4)   0   0   1 EP=   1 
5 P1: (5) 1/2 1/2   0 EP= 1/2 P2: (5) 1/2 1/2   0 EP= 1/2 
6 P1: (6)   0   1   0 EP=   1 P2: (6)   0   1   0 EP=   1 
7 P1: (7)   1   0   0 EP=   1 P2: (7)   1   0   0 EP=   1

The image and output above were generated with our software:

http://www.gametheoryexplorer.org/

For the best known lower bound on the maximal number of Nash equilibria in a non-degenerate bimatrix game (which is greater than $2^n-1$ for $n>5$) see:

B. von Stengel (1999), New maximal numbers of equilibria in bimatrix games. Discrete and Computational Geometry 21, 557-568.