Evaluate Algebraically: Sequences and Series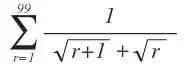

Question

Evaluate Algebraically (Sequences and Series):

possible duplicate of Find the sum $\frac{1}{\sqrt{1}+\sqrt{2}} + \frac{1}{\sqrt{2}+\sqrt{3}} + ...+ \frac{1}{\sqrt{99}+\sqrt{100}}$ — hardmath, May 24 '14 at 03:49

score 3 · Accepted Answer · answered May 24 '14 at 01:58

We have

$$\frac{1}{\sqrt{r+1}+\sqrt{r}}=\frac{\sqrt{r+1}-\sqrt{r}}{(\sqrt{r+1}+\sqrt{r})(\sqrt{r+1}-\sqrt{r})}=\frac{\sqrt{r+1}-\sqrt{r}}{r+1-r}=\sqrt{r+1}-\sqrt{r}.$$

So

$$\sum_{r=1}^{99}\frac{1}{\sqrt{r+1}+\sqrt{r}}=\sum_{r=1}^{99} (\sqrt{r+1}-\sqrt{r})=\sqrt{100}-\sqrt{1}=10-1=9.$$

Evaluate Algebraically: Sequences and Series

1 Answers1