I'm reading an ACL 2014 paper: Lei, Tao, et al. "Low-Rank Tensors for Scoring Dependency Structures.", ACL 2014.
It defines the Kruskal form of a tensor as a sum of Kronecker products:

However, http://www.ima.umn.edu/industrial/2006-2007/kolda/kolda.pdf defines the Kruskal form of a tensor as a sum of outer products:
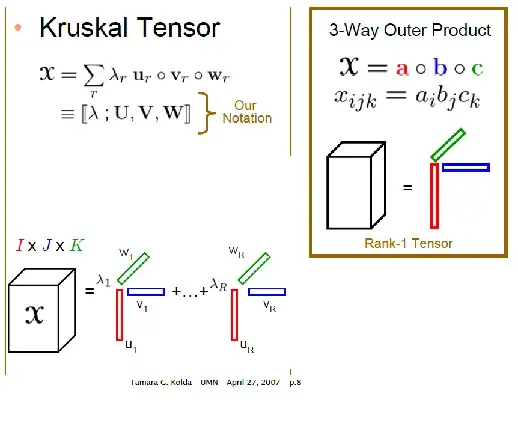
So should the Kruskal form of a tensor be defined as a sum of outer or Kronecker products?