Distance point on ellipse to centre

Question

I'm trying to calculate the distance of a certain point of an ellipse to the centre of that ellipse:

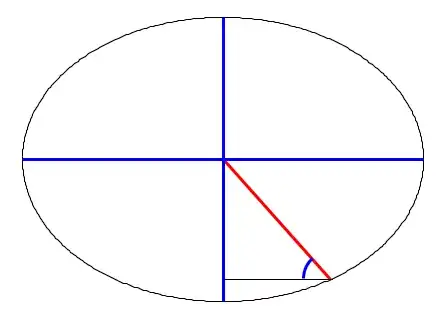
The blue things are known: The lengths of the horizontal major radius and vertical minor radius and the angle of the red line and the x-axis. The red distance is the desired result. It is not given where on the ellipse the point is. It can be anywhere on the ellipse. Is this problem possible? If so, in which can this be solved? Thanks in advance!

---

After reading Kaj Hansen's comment and trying a bit this is what I did, it still won't work though.

In a triangle, $tan(\theta)=\frac{\text{opposite side}}{\text{adjecent side}}$. The slope of a line is $\frac{\Delta y}{\Delta x}$. Therefor the slope of the red line is $\tan(\theta)$; the formula of the line is $y=\tan(\theta)\cdot x$.

The formula of the ellipse is $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1$. When I put the two formulas together I get $$\frac{x^{2}}{a^{2}}+\frac{(\tan(\theta)\cdot x)^{2}}{b^{2}}=1$$

After a bit of rearranging:

$$x=\pm \sqrt{\frac{a^{2}\cdot b^{2}}{a^{2}\cdot (\tan(\theta))^{2}+b^{2}}}$$

$$$$

$$y=\tan(\theta)\cdot x$$

$$y=\pm \tan(\theta) \cdot \sqrt{\frac{a^{2}\cdot b^{2}}{a^{2}\cdot (\tan(\theta))^{2}+b^{2}}} $$

Now with the help of Pythagoras' theorem $c=\sqrt{a^{2}+b^{2}}$ the red line should be

$$\sqrt{\left ( \sqrt{\frac{a^{2}\cdot b^{2}}{a^{2}\cdot (\tan(\theta))^{2}+b^{2}}}\right ) ^{2}+\left ( \tan(\theta) \cdot \sqrt{\frac{a^{2}\cdot b^{2}}{a^{2}\cdot (\tan(\theta))^{2}+b^{2}}} \right )^{2}}$$

which can be simplified:

$$\sqrt{\frac{a^{2}\cdot b^{2} \cdot (\tan(\theta))^{2}+a^{2}\cdot b^{2}}{a^{2}\cdot (\tan(\theta))^{2}+b^{2}}}$$

This, however, does not give the right answer. Let's try something:

$a=2$; $b=1$; $\theta=\frac{1}{2}\cdot \pi$ (The point is the point where the ellipse intersects with the minor radius)

$$\sqrt{\frac{2^{2}\cdot 1^{2} \cdot (\tan(\frac{1}{2}\cdot \pi))^{2}+2^{2}\cdot 1^{2}}{2^{2}\cdot (\tan(\frac{1}{2}\cdot \pi))^{2}+1^{2}}}$$

$$\sqrt{\frac{4 \cdot (\tan(\frac{1}{2}\cdot \pi))^{2}+4}{4\cdot (\tan(\frac{1}{2} \pi))^{2}+1}}$$

But wait, $\tan(\frac{1}{2}\cdot \pi)$ is undefined. The formula cannot be filled in completely, which is a requirement. I need a formula that can be filled in for every value of $\theta$ on the domain $[0,\frac{1}{2}\cdot \pi]$

Answer 1

A more straightforward method is to convert the coordinates to their parametric form:

$$x=a\cos\theta$$ $$y=b\sin\theta$$

where $\theta$ is the angle made by the point to the center and the $x$-axis, and is thus equal to the angle you have shown. The distance from the center is then:

$$\sqrt{x^2 + y^2} = \sqrt{a^2\cos^2\theta+b^2\sin^2\theta}.$$

Answer 2

If $a$ is the length of the horizontal axis and $b$ the vertical axis, then the equation for the ellipse is $(x/a)^2 + (y/b)^2 = 1$.

From here, we can also get an equation for the red line since its slope is $\tan(\theta)$ and $y$-intercept is $0$.

To find the point where the line intersects the ellipse, simply take the equation of the line, $y = mx$, and plug it into the equation for the ellipse, $(x/a)^2 + (y/b)^2 = 1$, and solve for $x$ (note that this will give two possible values). Then, you can plug the appropriate $x$-value back into the ellipse formula to get the corresponding $y$-coordinate.

Now that you have the point of intersection, simply use the Pythagorean theorem to obtain the length of the red segment.

Answer 3

We know that the Parametric equation of an Ellipse - not centered, and not parallel to the Axises - is: $$ x(\alpha) = R_x \cos(\alpha) \cos(\theta) - R_y \sin(\alpha) \sin(\theta) + C_x \\ y(\alpha) = R_x \cos(\alpha) \sin(\theta) + R_y \sin(\alpha) \cos(\theta) + C_y $$

Where:
- $C_x$ is center X.
- $C_y$ is center Y.
- $R_x$ is the major radius.
- $R_y$ is the minor radius.
- $\alpha$ is the parameter, which ranges from 0 to 2π radians.
- $\theta$ is the Ellipse rotation angle.

You can see this equation explanation here: What is the parametric equation of a rotated Ellipse (given the angle of rotation)

So all you need to do is enter your parameters to this equation to find the point (X, Y) and calculate the distance fron the Ellipse center to point (X, Y) on the Ellipse edge.

Distance equation: $$ distance = \sqrt{(x_1 - x_2) ^ 2 + (y_1 - y_2) ^ 2} $$

Answer 4

I'm assuming that the centre is located on the origin.

Let us call the point where the red line meets the ellipse P. Let P have coordinates $(x_1, y_1) $. Notice that $tan\theta = y_1/x_1$. Let the horizontal semi-axis be $a$, meaning the ellipse is $2a$ wide. Similarly, let the vertical semi-axis be $b$. Let the known blue angle be $\theta$.

Equation of an ellipse(centered at origin) =

$x^2/a^2 + y^2/b^2 = 1$

Since $(x_1,y_1)$ satisfies the equation, the equation becomes:

$x_1^2/a^2 + y_1^2/b^2 = 1$

But $tan\theta = y_1/x_1$ so $y_1^2 = x_1^2tan^2\theta$. Substituting this:

$x_1^2/a^2 + x_1^2tan^2\theta/b^2 = 1$
$x_1^2(1/a^2 + tan^2\theta/b^2) = 1$
$x_1^2(\frac{a^2tan^2\theta+b^2}{a^2b^2}) = 1$
$x_1^2= \frac{a^2b^2}{a^2tan^2\theta+b^2}$

Finding the value of $y_1^2$, we get:
$y_1^2 = \frac{a^2b^2}{a^2tan^2\theta+b^2}\times tan^2\theta$
$y_1^2 = \frac{a^2b^2tan^2\theta}{a^2tan^2\theta+b^2}$

Since we have assumed the centre to be the origin, the distance becomes:
$\sqrt{x_1^2+y_1^2}$
$\sqrt{\frac{a^2b^2}{a^2tan^2\theta+b^2}+\frac{a^2b^2tan^2\theta}{a^2tan^2\theta+b^2}}$
Since $1+tan^2\theta = sec^2\theta$, we have:
$\sqrt{\frac{a^2b^2sec^2\theta}{a^2tan^2\theta+b^2}}$

Addressing your problem, note that both tan and sec don't have continuous domains, however, both of them have cos as the denominator in one or the other representation. So, we can multiply both the numerator and denominator by $cos\theta$ to get rid of the discontinuous domain.

$\sqrt{\frac{a^2b^2sec^2\theta}{a^2tan^2\theta+b^2}}\times\sqrt{\frac{cos^2\theta}{cos^2\theta}}$
$\sqrt{\frac{a^2b^2}{a^2sin^2\theta+b^2cos^2\theta}}$
$\frac{ab}{\sqrt{a^2sin^2\theta+b^2cos^2\theta}}$
You could rationalize the denominator if you want. This formula works for $\theta = \pi/2$

Note: Even though we have assumed the ellipse to be centred at origin, the formula still works as any other ellipse with same a,b would be congruent to the discussed one.

Answer 5

Convert the equation of ellipse from rectangular to polar coordinates.

$ (x/a)^2 + (y/b)^2 = 1 $ , $ x = r cos(\theta), y = r sin(\theta)$.

$ (cos(\theta)/a )^2+ (sin(\theta)/b)^2 =1/r^2 $.

$(a,b,\theta )$ are given. Find out 1/$r^2$ and $r$.