Klein Bottle Embedding on $\mathbb{R}^4$.

Question

First of all, I am aware of the question in How to embed Klein Bottle into $R^4$ , which was inconclusive. Anyway, I've made some progress, but I still have a question.

I am using Do Carmo's Riemannian Geometry, and struggling to solve a problem.

The problem is:

Show that the mapping $G:\mathbb{R}^2\to\mathbb{R}^4$ given by

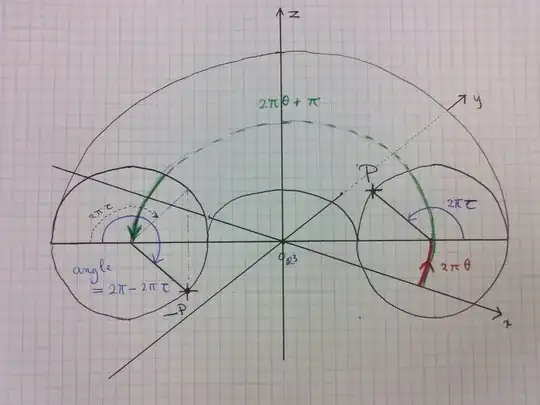
$$G(x,y)=((r\cos (2\pi y)+a)\cos (4\pi x),(r\cos (2\pi y)+a)\sin (4\pi x),r\sin (2\pi y)\cos (2\pi x),r\sin (2\pi y)\sin (2\pi x)))$$

induces an embedding of the Klein bottle into $\mathbb{R}^4$ (It is a slightly different function from the one in the book, but works in the same way).

First of all, it's not hard to see that $$G(x+n,y+m)=G(x,y)\text{ whenever }m,n\in\mathbb{Z}.$$ Therefore, this mapping is well-defined over the torus $\mathbb{T}^2$. What I need now is to show that $G(-x,-y)=G(A(x,y))=G(x,y)$, where $A$ is the antipode mapping. If this were true, then the mapping G would be well-defined over the Klein Bottle, but it's obvious that this is false.

Am I working wrong here somewhere?

Answer 1

Consider the embedding $\psi:\Bbb R\times\Bbb R\big/{\Bbb Z\times\Bbb Z}\hookrightarrow\Bbb R^3$ $$\psi([\theta, \tau])= \begin{pmatrix} \cos(2\pi\theta) &-\sin(2\pi\theta) & 0\\ \sin(2\pi\theta) &\cos(2\pi\theta) & 0\\ 0&0&1 \end{pmatrix} \begin{pmatrix} 2+\cos(2\pi\tau)\\ 0\\ \sin(2\pi\tau) \end{pmatrix}$$ Then one verifies (on the picture and then by doing the math) that $-\psi([\theta, \tau])=\psi([\theta+\frac12, -\tau])$

Thus the Klein bottle is the quotient of $\Bbb R\times \Bbb R$ by the (non-commutative) group $H=\langle v,t\rangle$ of homeomorphisms generated by the vertical displacement by one $$v(\theta, \tau)=(\theta, \tau + 1)$$ and a twist $$t(\theta, \tau)=(\theta+\frac12, -\tau).$$ Notice that $t^2=h$ the horizontal displacement by one $h(\theta, \tau)=(\theta + 1, \tau)$.

You'll verify that $G(v(\theta, \tau))=G(\theta, \tau)=G(t(\theta, \tau))$, so $G$ descends to a map $\tilde{G}:K\to \Bbb R^4$. $\tilde{G}$ is an injective (easy verification) immersion ($G$ already was). By compactness of $K$, it is an embedding.

Answer 2

This is not a separate answer, but a long comment to Olivier Bégasset's answer.

Just for sake of completeness, let us give here the elementary proof that the map $\tilde{G}$ defined in the answer given by Olivier Bégasset is actually injective. Assume that $(x,y), (\bar{x},\bar{y}) \in \mathbb{R}^2$ are such that \begin{cases} (r\cos (2\pi y)+a)\cos (4\pi x)=(r\cos (2\pi \bar{y})+a)\cos (4\pi \bar{x}) \\ (r\cos (2\pi y)+a)\sin (4\pi x)=(r\cos (2\pi \bar{y})+a)\sin (4\pi \bar{x}) \\ r\sin (2\pi y)\cos (2\pi x)=r\sin (2\pi \bar{y})\cos (2\pi \bar{x})\\ r\sin (2\pi y)\sin (2\pi x)=r\sin (2\pi \bar{y})\sin (2\pi \bar{x}). \end{cases} By squaring the two members of the first two equations and summing up, you get \begin{equation} (r\cos (2\pi y)+a)^2=(r\cos (2\pi \bar{y})+a)^2, \end{equation} while by squaring the two members of the last two equations and summing up, you get \begin{equation} \sin^2(2\pi y)=\sin^2(2\pi \bar{y}). \end{equation} From the last two equations you easily get $$ (I) \qquad \cos(2 \pi y)= \cos (2\pi \bar{y}). $$ If we use (I) in the first two equations of the system, we get $$ x=\bar{x}+\frac{m}{2}, \qquad (m \in \mathbb{Z}). $$ Now, if $m$ is even, from the last two equations of the system we get $$ (II) \qquad \sin(2 \pi y)= \sin (2\pi \bar{y}), $$ so that from (I) and (II) we deduce that $y=\bar{y}+n$, with $n \in \mathbb{Z}$, hence $(x,y)$ and $(\bar{x},\bar{y})$ belong to the same H-orbit. If insted $m$ is odd, from the last two equations of the system we get $$ (III) \qquad \sin(2 \pi y)= -\sin (2\pi \bar{y}), $$ so that from (I) and (III) we deduce that $y=n-\bar{y}$, with $n \in \mathbb{Z}$, and again $(x,y)$ and $(\bar{x},\bar{y})$ belong to the same H-orbit.