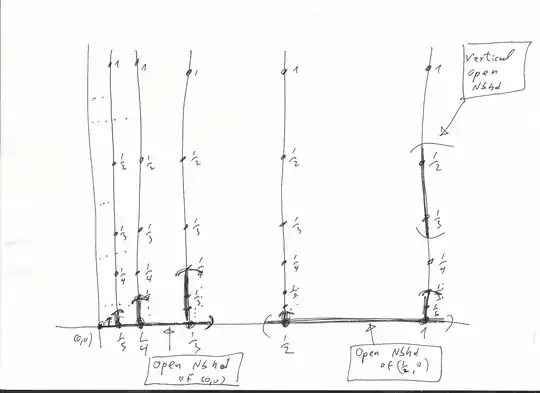
The space is sequential but not Fréchet–Urysohn.
To give a perhaps more concise definition of the space, let $$\newcommand{\angles}[1]{\langle {#1} \rangle}
X = \{ \angles{0,0} \} \cup \{ \angles{\tfrac{1}{i} , 0 } : i \geq 1 \} \cup \{ \angles{ \tfrac{1}{i} , \tfrac{1}{j} } : i,j \geq 1 \},$$ and topologise $X$ by the declaring the following families of basic open neighbourhoods:
- each $\angles{ \frac{1}{i} , \frac{1}{j} }$ is isolated;
- basic open neighbourhoods of $\angles{ \frac{1}{i} , 0 }$ are of the form $\{ \angles{ \frac{1}{i} , 0 } \} \cup \{ \angles{ \frac{1}{i} , \frac{1}{j} } : j \geq k \}$ some some $k \geq 1$;
- basic open neighbourhoods of $\angles{0,0}$ are of the form $\{ \angles{0,0} \} \cup \bigcup_{i \geq \ell} U_i$ where $\ell \geq 1$ and $U_i$ is a basic open neighbourhood of $\angles{\frac{1}{i} ,0}$ for each $i \geq \ell$.
Claim. $X$ is not Fréchet–Urysohn.
sketch. Let $A = \{ \angles{ \frac{1}{i} , \frac{1}{j} } : i , j \geq 1 \}$. Clearly $\angles{0,0} \in \overline{A}$. Suppose that $\angles{ x_n = \angles{ i_n^{-1} , j_n^{-1} } }_{n=1}^\infty$ is any sequence in $A$. If $\{ i \in \mathbb{N} : ( \exists n ) ( i_n = i ) \}$ is finite, then it is easy to construct an open neighbourhood of $\angles{0,0}$ not containing any element of the sequence. Otherwise by passing to a subsequence we can assume that $i_n < i_{n+1}$ for all $n$, and from here construct a basic open neighbourhood of $\angles{0,0}$ disjoint from this subsequence.
Claim. $X$ is sequential.
sketch. Let $A \subseteq X$ contain all the limits of convergent sequences in $A$. We wish to show that $A$ is closed; i.e., $\overline{A} \subseteq A$. Suppose that $x \in \overline{A}$. Note that if $x \neq \angles{0,0}$, then as there is a countable base at $x$ it is straightforward to show that there is a sequence in $A$ converging to $x$, and so $x \in A$. So let's assume that $\angles{0,0} \in \overline{A} \setminus A$. We can show that the set $$\{ i \geq 1 : \text{every open nbhd of }\angles{\tfrac{1}{i},0}\text{ intersects }A \}$$ is infinite (since otherwise we could construct an open neighbourhood of $\angles{0,0}$ disjoint from $A$), and so we may enumerate it increasingly as $\angles{ i_n }_{n=1}^\infty$. But then for each $n \geq 1$ we have that $\angles{ i_n^{-1} , 0 } \in \overline{A}$, and therefore by the above observation $\angles{ i_n^{-1} , 0 } \in A$. It is then easy to see that $\angles{ \angles{i_n^{-1} , 0} }_{n=1}^\infty$ is a sequence in $A$ converging to $\angles{0,0}$, and so $\angles{0,0} \in A$, contradicting our assumption that it is not!