Examples of Cohen-Macaulay rings.

Question

I've just started to learn about Cohen-Macaulay rings. I want to show that the following rings are Cohen-Macaulay:

$k[X,Y,Z]/(XY-Z)$ and $k[X,Y,Z,W]/(XY-ZW)$.

Also I am looking for a ring which is not Cohen-Macaulay.

Can anyone help me?

Answer 1

a) The ring $k[X,Y,Z]/(XY-Z)$ is isomorphic to the ring $k[X,Y]$, which is regular.
Since a regular ring is Cohen-Macaulay, the original ring $k[X,Y,Z]/(XY-Z)$ is Cohen-Macaulay.

b) The ring $k[X,Y,Z,W]/(XY-ZW)$ is a complete intersection ring and is consequently Cohen-Macaulay. [By the way, this argument also applies to the ring in a)]

c) The ring $R=k[x,y]:=k[X,Y]/(X^2, XY)$ (the usual suspect !) is not Cohen-Macaulay because its localization $R_\mathfrak m=k[x,y]_\mathfrak m$ at the maximal ideal $\mathfrak m=(x,y)\subset R$ is not Cohen-Macaulay:
Indeed every element $f\in \mathfrak m R_\mathfrak m=(x,y)$ is a zero divisor since $x\neq0$ but $fx=0$ (recall that $x^2=xy=0$).
So there are no regular sequences at all in the local ring $R_\mathfrak m$, which consequently is not Cohen-Macaulay.

c') Another, stunningly geometric, example of a non Cohen-Macaulay ring is the ring $A=k[x,y,z]:=\Gamma(V,\mathcal O_V)$ of global functions on the closed algebraic subset $V\subset \mathbb A^3$ consisting of the union of a plane and a transverse line, say $A=k[X,Y,Z]/(ZX,ZY)$.
The localization $A_\mathfrak m$ of $A$ at the maximal ideal $\mathfrak m=(x,y,z)$ (corresponding to the singularity of $V$) is obviously not equidimensional and thus $A_\mathfrak m$ is not Cohen-Macaulay.
This example is lifted from Eisenbud, Corollary 18.11 .

Answer 2

bruns herzog book Cohen Macaulay rings

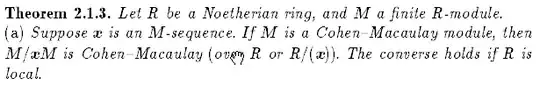
note that the rings $k[X,Y,Z]$ and $k[X,Y,Z,W]$, are integral domains and each nonzero element of them is a regular sequence.