1

So there is an example problem in the textbook and I really just don't understand what's going on, both mathematically and conceptually. The problem is solve $z_x + 2zz_y = 1$ with boundary conditions $z = 0$ on $y=0$ for $x \ge 0$ and $z=y$ on $x=0$ for $y \ge 0$.

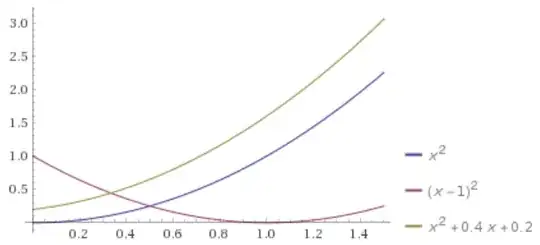
I write the characteristic problem as $x_s = 1$, $y_s = 2z$, and $z_s = 1$. With the first boundary condition, we can write the line $\Gamma(\sigma) = (\sigma, 0, 0)$ therefore we get that $x = s + \sigma$, $y = s^2$, and $z = s$. Therefore we get characteristic curves $y = (x-\sigma)^2$. Then the textbook implies that the solution is only specified below the parabola $y = x^2$. I don't understand this. Also, given these characteristics, there will be infinitely many characteristic intersections below the parabola $y = x^2$, so this makes me think the solution is not specified at those points either.

Can anyone reconcile this or give me some guidance on what's going on here?

EditPiAf
  • 21,328
user137302
  • 296

2 Answers2

2

Here, the boundary data is specified on the two orthogonal half-lines $x=0, y\geq 0$ and $y=0, x\geq 0$. We must compute the characteristic curves coming from each boundary (see e.g. this post).

The first family of characteristic curves issued from the boundary $x=0$ where $z=y$ is the set of curves $y = x^2 + 2 y_0 x + y_0$ with $y_0\geq 0$, along which $$ z = x+y_0 = \frac{x^2 + x + y}{1+2x} . $$ The second family of characteristic curves issued from the boundary $y=0$ where $z=0$ is the set of curves $y = (x-x_0)^2$ with $x_0\geq 0$, along which $$ z = x-x_0 = \sqrt{y} . $$ Plotting the characteristic curves in the $x$-$y$ plane, we get the figure

characteristics

One can observe that the solution is uniquely defined in the region $y\leq x^2$. Indeed, two characteristic curves may intersect, but they carry the same information $z = \sqrt{y}$. However, the solution is not uniquely defined in the region $y> x^2$ where characteristic curves carrying different information intersect. In that region, it is required to introduce weak solutions since the classical solution is no longer well-defined.

EditPiAf
  • 21,328
1

Follow the method in http://en.wikipedia.org/wiki/Method_of_characteristics#Example:

$\dfrac{dx}{dt}=1$ , letting $x(0)=0$ , we have $x=t$

$\dfrac{dz}{dt}=1$ , letting $z(0)=z_0$ , we have $z=z_0+t=z_0+x$

$\dfrac{dy}{dt}=2z=2z_0+2t$ , letting $y(0)=f(z_0)$ , we have $y=f(z_0)+2z_0t+t^2=f(z-x)+2(z-x)x+x^2=f(z-x)-x^2+2xz$ , i.e. $z=x+F(x^2-2xz+y)$

$z(0,y)=y$ :

$F(y)=y$

$\therefore z=x+x^2-2xz+y$

$2xz+z=x^2+x+y$

$(2x+1)z=x^2+x+y$

$z(x,y)=\dfrac{x^2+x+y}{2x+1}$

But this solution does not satisfy $z(x,0)=0$ ,

$\therefore$ the concept of piecewise solution should be introduced

doraemonpaul
  • 16,488