If $X$ and $Y$ are independent normally distributed random variables
$$X,Y\sim\mathcal{N}(0,\sigma^2)$$
How are the sum and product, $X+Y$ and $XY$, co-distributed? You can write the moment generating function
$$V=X+Y\qquad Z=XY$$ \begin{align} M_{V,Z}(s,t)&=\int _{-\infty }^{\infty }\int _{-\infty }^{\infty }\exp\left[s (v+z)+t (vz)\right]\psi (v,0,\sigma^2) \psi (z,0,\sigma^2)\mathrm{d}v\mathrm{d}z\\ &=\frac{\exp\left[\dfrac{s^2 \sigma ^2}{1-\sigma ^2 t}\right]}{\sqrt{1-\sigma ^4 t^2}} \end{align}
But I do not know what probability density function this belongs to, besides that it looks like the MGF for a modified Bessel function of the second kind and normal distribution. Attached is a histogram generated from $10^7$ such pairs of random numbers.
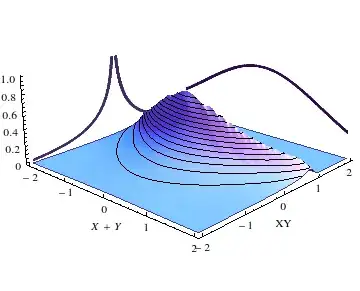
EDIT: Turns out Mathematica can handle this thing, and spits this monster out $$f(v,z;\sigma^2)=\frac{\sqrt[4]{-1} \left[\sqrt{-i \left(v^2-4 z\right)}-i \sqrt{i \left(v^2-4 z\right)}\right] }{\left| v^2-4 z\right| }\frac{\exp\left(-\dfrac{v^2-2 z}{2 \sigma ^2}\right)}{2 \pi \sigma ^2}$$ Does anyone know if this related to some well-known result I could read around?
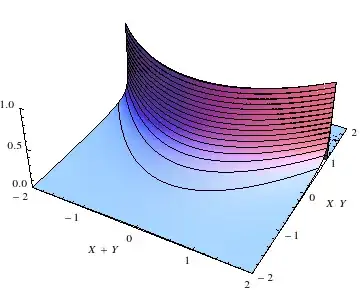
The function Mathematica spat at me appears to be the solution, I've simply never encountered this flavour of distribution before.
– user5751 Apr 08 '14 at 18:42