Proof of Parseval's Theorem for Fourier Series

Question

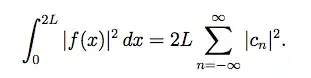
Ok so I want to prove the above expression, I substituted the complex fourier series for f and using the fact f may be complex-valued, carried on by representing $|f(x)|^2$ as $f(x)f(x)^\ast$ where the ast represents complex conjugation. The problem is when now I substitute the complex fourier series I get three summations, one is the one above and two more by matching the powers of the exponentials. The two extra summations are below:

$2L\sum_{n=-\infty}^{\infty}C_nC_{-n}^\ast+2L\sum_{n=-\infty}^{\infty}C_{-n}C_{n}^\ast$

Answer 1

Assuming the usual (inner product $\;\langle,\rangle\;$, orthonormal basis $\;\{u_i\}\;$ and etc.):

$$\frac1{2L}\int\limits_0^{2L}|f(x)|^2dx=\langle f(x)\,,\,f(x)\rangle=\sum_{k=-\infty}^\infty\sum_{m=-\infty}^\infty c_k\overline{c_m}\langle u_k\,,\,u_m\rangle=\sum_{k=-\infty}^\infty|c_k|^2$$

Of course, we usually have that the $\;u_i$'s are the complex exponentials and etc., and the above follows from the basic orthonormality relations

$$\langle u_k\,,\,u_m\rangle=\delta_{km}:=\begin{cases}1&,\;\;\;k=m\\{}\\0&,\;\;\;k\neq m\end{cases}$$