2

Source: Stewart, James. Calculus: Early Transcendentals (6 edn 2007). p. 1097. §16.8, Exercise #5.

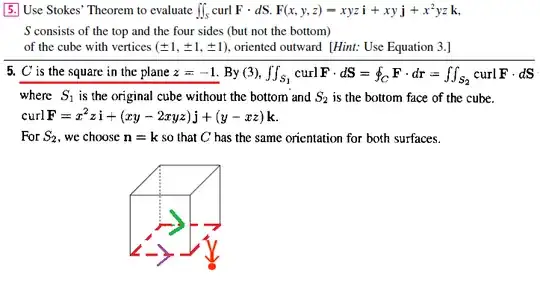
enter image description here

$\Large{1.}$ How does one determine the boundary curve, called C, to be the plane $z = -1$? I don't understand, as $S$ here is given as bottomless.

$\Large{2.}$ Why isn't the unit normal vector for $S_2$ be $-\mathbf{k}$ ? How does one determine which direction, either green or purple, is correct for the red person, without flipping the figure vertically?

Can someone please explain more informally than Christian Blatter's answer that looks too complicated?

2 Answers2

2

Stokes' theorem says that for a force field ${\bf F}$ and a $2$-chain $S$ with boundary $\partial S$ embedded in ${\rm dom}({\bf F})$ one has $$\int_S {\rm curl}\,{\bf F}\cdot d\vec\omega=\int_{\partial S} {\bf F}\cdot d{\bf x}\ .\tag{1}$$ In our example $S$ is a union of five squares $S_j$, and the $\partial S_j$ cancel, up to four segments making up a square shaped $1$-chain $\partial Q$ in the plane $z=-1$. This $1$-chain, as seen from above, runs counterclockwise around $Q$. When we now apply Stokes' theorem again, this time to $Q$, the correct choice of the positive normal will therefore be upwards.

It follows that we can continue formula $(1)$ by $$\int_{\partial S} {\bf F}\cdot d{\bf x}=\int_{\partial Q} {\bf F}\cdot d{\bf x}=\int_Q {\rm curl}\,{\bf F}(x,y,-1)\cdot(0,0,1)\ {\rm d}(x,y)\ .$$ According to the givens, $${\rm curl}\,{\bf F}(x,y,-1)\cdot(0,0,1)=y+x\ , $$ and integrating the latter over $Q$ gives $0$, by symmetry.

(In the above the word chain means that we are not talking about a single smooth surface or curve, but with "formal sums" of such things. The $S$ in the original formulation of the problem is a $2$-chain. Its boundary $\partial S$ is the "sum" of the $\partial S_j$ of the constituent squares and amounts to the $1$-chain $C=\partial Q$.)

Christian Blatter
  • 232,144
  • Thank you. My course doesn't involve "chains", so would you please exclude them from your answer? Also, we never defined or learned about the boundary $\partial_Q$. Would you please exclude it as well? Will you please to respond in your answer, and not as comments? –  Apr 22 '14 at 08:38
1

$(1)$ since the cube is bottomless, the square at the bottom of the cube is the boundary. This square lies in the plane $z=-1$, but it is not the whole plane.

$(2)$ firstly, your green and purple arrows are going in the same direction, so lets just imagine the green one is pointing the other way.

Both $n=k$ and $n=-k$ are normal to $C$, you can take either as long as the person is walking around the surface in the right way (discussed below).

The way to determine the correct direction (looking from below) is to imagine that the interior of the surface must always be on the person's left (as they walk around the boundary) which corresponds with the green direction.

    
I was explaining the direction choice for $n=−k$, so that it matched your picture, the example uses $n=k$, so the direction changes (from green to purple), this is so we can go around the boundary in the same directions for both surfaces $S_1$ and $S_2$.

Ellya
  • 12,149
  • Thanks. Regarding your last paragraph though, are you looking from above or below the $z = 1 plane$ ? Because from below, the green (now fixed) direction is right. Please explain how you chose the point of view? –  Jun 01 '14 at 13:37
  • I have edited, you were right it is the green direction, I got confused because it is upside down :) – Ellya Jun 01 '14 at 13:53
  • Thanks, but why must we look from below $z = -1$? And NOT above it? –  Jun 01 '14 at 13:54
  • I was explaining the direction choice for $n=-k$, so that it matched your picture, the example uses $n=k$, so the direction changes (from green to purple), this is so we can go around the boundary in the same directions for both surfaces $S_1$ and $S_2$. – Ellya Jun 01 '14 at 13:58
  • OK, thanks. Would you please respond to my supplementaries at http://math.stackexchange.com/q/739328/53259, under your answer? –  Jun 01 '14 at 14:04
  • Also, please move your comments into your answers? –  Jun 01 '14 at 14:05
  • I have moved them :) – Ellya Jun 01 '14 at 14:10
  • @LePressentiment, is this sufficient? :) – Ellya Jun 05 '14 at 21:28
  • Yes, thank you! –  Jun 06 '14 at 21:32