This is something that always annoys me when putting an A4 letter in a oblong envelope: one has to estimate where to put the creases when folding the letter. I normally start from the bottom and on eye estimate where to fold. Then I turn the letter over and fold bottom to top. Most of the time ending up with three different areas. There must be a way to do this exactly, without using any tools (ruler, etc.).
13 Answers
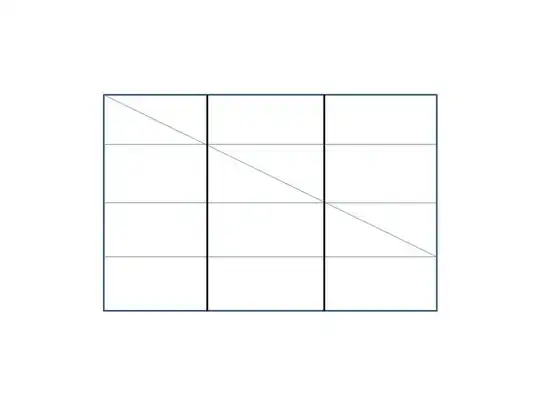
Fold twice to obtain quarter markings at the paper bottom. Fold along the line through the top corner and the third of these marks. The vertical lines through the first two marks intersect this inclined line at thirds, which allows the final foldings.
(Photo by Ross Millikan below - if the image helped you, you can up-vote his too...)
- 201
- 382,479
-
1Do you have any drawings or photos of how to do this? for example, I can't tell whether the first 2 folds are parallel or perpendicular to the long side. – Nzall Apr 02 '14 at 13:06
-
27Perfect! I'll use this method for all business correspondence from now on =) – Jens Apr 02 '14 at 14:02
-
@NateKerkhofs The first two folds are parallel to the long side; the next fold then creates a diagonal line from one corner to the third mark, and the intersection of this line with the other two marks then divide this line (and thus the long axis of the sheet) into thirds. – Steven Stadnicki Apr 02 '14 at 15:21
-
52And of course this has the advantage of utterly befuddling the recipient. – E.P. Apr 02 '14 at 21:12
-
44Keep a "template" like this handy so that you don't send the worlds most creased correspondence. – Daniel E. Apr 03 '14 at 00:04
-
15
- With this method one can fold a letter an arbitrary number of times (if one does not reach physical limits ). So if one wants to fold it in 5 equal parts one first folds it in $2^3=8$ equal parts and the folds along the line through the top corner and the 5th mark. 2) One must use the second dimensions. When folding only parallel to one side one cannot fold into 3 equal parts. It is not possible to partition an interval $[0,1]$ in three equal parts by bisecting . The points that you can construct this way are $0,1$ and points of the form $\frac{n}{2^k}$.
– miracle173 Apr 03 '14 at 05:43 -
6My results are significantly better if I fold three times to get the quarter markings (fold in half, unfold, fold each half in half). Following the letter(!) of your method as currently written I am off by almost half an inch every time. The diagonal fold is fairly difficult to get right as well, since there is nothing with which to line up the end of the paper as you fold, just a page corner on one side and crease/border intersection on the other. I love the elegance and generalizability, but 5 or 6 folds make this about as reliable as the default "flatten the tube" method in practice. – Tyler James Young Apr 03 '14 at 19:22
-
2
-
1Nice. One point to note is that this is not A4 specific (actually none of the answers is). – leonbloy Apr 06 '14 at 19:48
-
I need some practice. I used this method first, then did another sheet 'by eye'. Both were roughly 2 mm off. ;-) – Henk Langeveld Apr 07 '14 at 12:31
-
And if I'm not mistaken, this will work no matter the dimensions of the paper used! And it's easy to see how to get any other fraction! Cool! – Thomas Ahle Jun 10 '14 at 08:19
-
Here is a picture to go with Hagen von Eitzen's answer. The horizontal lines are the result of the first two folds. The diagonal line is the third fold. The heavy lines are the points at thirds for folding into the envelope.

- 383,099
-
19Shouldn't this be an edit to the previous answer, not a separate answer by itself? – Etheryte Apr 02 '14 at 19:38
-
3
-
1@Nit: I thought about editing it in, but didn't want to do it over Hagen von Eitzen's signature. I didn't think he would mind, but I don't have a way to be sure. – Ross Millikan Apr 02 '14 at 19:56
-
@user973810 An accepted answer should be self-contained, much like a good question, this post isn't really an answer, rather a comment in my opinion. – Etheryte Apr 02 '14 at 20:50
-
9@RossMillikan If you edit someone's post their signature isn't overwritten, the original poster is still shown next to the edit information. – Etheryte Apr 02 '14 at 20:51
-
4
-
-
@Chris Text that is "over" someone's signature is physically above it on the page and so is understood to have been endorsed by the signer. It's common usage when the actual author of a document is different from the person under whose authority it's promulgated; e.g., an official's staff may prepare reports for publication over that official's signature. Millikan didn't want to leave the impression that von Eitzen had produced or endorsed Millikan's diagram. – Apr 04 '14 at 14:13
-
@StevenTaschuk: Ah, that makes sense and is pretty obvious now you say it and makes a lot of sense. – Chris Apr 04 '14 at 14:33
-
By the way, this figure represents a rotated (and possibly flipped) version of the words in Hagen von Eitzen's answer. – ShreevatsaR Apr 07 '14 at 04:45
-
-
@GilbertS: There is an explanation in Hagen von Eitzen's answer. The third comment there lists the steps. – Ross Millikan Dec 03 '20 at 17:32
This is both practical (no extra creases) and precise (no guessing or estimating).
Roll the paper into a 3-ply tube, with the ends aligned:
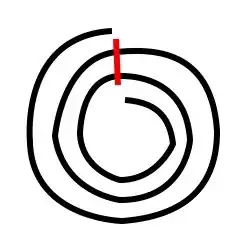
Pinch the paper (crease the edge) where I've drawn the red line
Unroll
Use the pinch mark to show where the folds should be
-
20This is also nice in that it doesn't leave the paper with extraneous creases. – Nate Eldredge Apr 03 '14 at 19:22
-
5No extra creases. Exactly the right place. Quick to execute. Works for any size paper. This is clearly the best answer. – Sam Dickson Apr 04 '14 at 13:00
-
16But the "outermost" third will be slightly larger than the middle one (and that one than the innermost one), by at least $2\pi$ times the thickness of the paper. (More if rolling up actually resembles the illustration.) – Marc van Leeuwen Apr 04 '14 at 13:01
-
51@MarcvanLeeuwen True, but for very important correspondence (that which must be folded exactly into thirds) one would generally use an ideal sheet of paper with 0 thickness, so that wouldn't be a problem. – Reinstate Monica -- notmaynard Apr 04 '14 at 15:16
-
8@MarcVanLeeuwen But as anyone who's experienced the pain of designing a tri-fold brochure will know, this is exactly what you want! (Well for those folded like a 6, not a Z.) The third that you fold first should be the smallest (by a mm or so) so that it's not squished and damaged inside the second fold. And it allows the final edge to align nicely with the first fold and not fall short. Love this solution! – Simon East Apr 04 '14 at 23:30
-
1@Simon - thanks for explaining this, I didn't have time when the objection was first posted. It's very annoying when you measure things 'exactly' but then the fold doesn't actually work because the paper is not infinitely thin. – egrunin Apr 06 '14 at 07:03
-
We have to neglect thickness, because otherwise you can't mathematically fold a paper with non-zero thickness anyway. Try to fold a one inch thick piece of paper aka a block of wood. You'd need a jigsaw and cut it in two halves. And there is no mathematical difference between an inch and a 10th of a millimetre. Thickness is either zero or non-zero. – gnasher729 Apr 06 '14 at 19:14
This solution works only with a sheet of paper having aspect ratio of sqrt(2) (as A4 has).
Only two extra folds required.
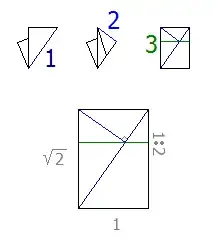
- 1,339
-
1One more fold allows this to work for any aspect ratio; see my answer below. – dvitek Jan 02 '23 at 09:34
- Roll in to a cylinder until both edges are opposite to each other.
- Fold the points where the edges touches the paper. (Squish the cylinder from left and right)

Approximation method:
- Assume a 120 degree angle and fold as shown below.
- For accuracy, match edge-side to any of the other two sides.

- 734
-
4Estimating when the two ends are diametrically opposite on a not-quite-circle isn't much easier than just estimating where to fold while looking at a flat piece of paper. – David Richerby Apr 05 '14 at 12:10
-
1I think this is a description of how everyone already folds paper, rotated 90 degrees. – Phil Apr 05 '14 at 17:40
Beyond the more geometric methods explained so far, there is an iterative algorithm (in practice, as precise as any exact method) due to Shuzo Fujimoto that I think no one mentioned. In fact, the following method can be generalized to any shape, size and number of foldings.
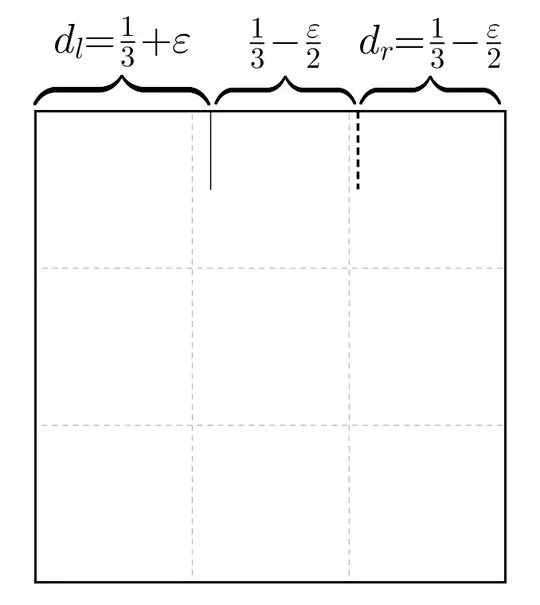
Let me denote $d_l$ the distance from the left side of the paper to the first mark on the left and $d_r$, the distance from the right side to the right mark. To simplify, assume that the lenght of the side you want to divide is 1.
Make a first approximation for $d_l$. You want $1/3$, but imagine you take $1/3+\varepsilon$ ($\varepsilon$ being some error to the right or to the left). Thus, on the right you now have $2/3-\varepsilon$.
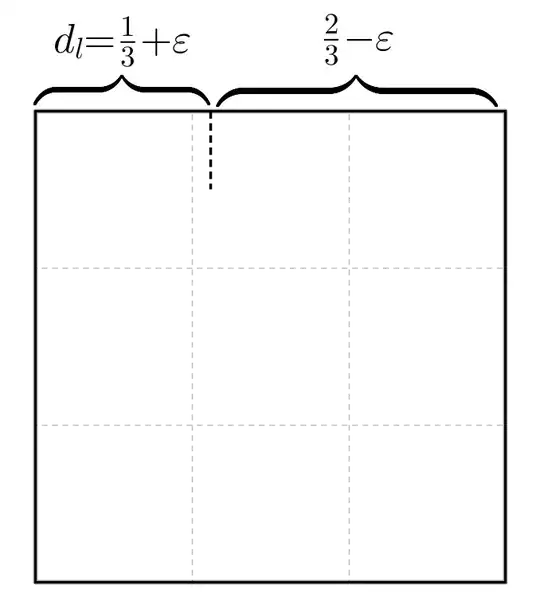
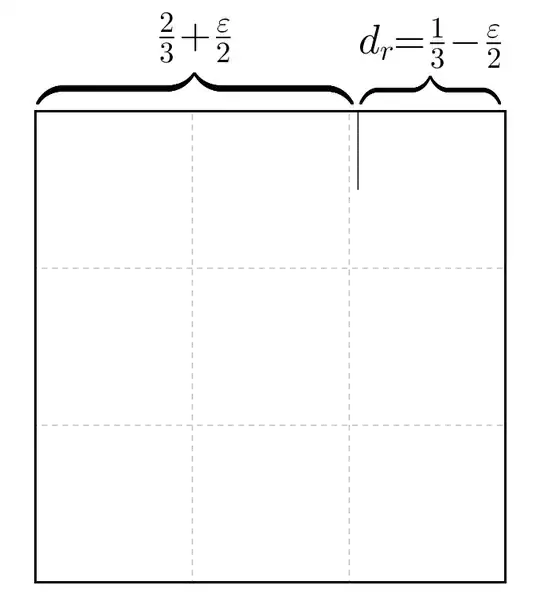
Next, divide the right part into two for the first approximation of $d_r$ (by taking the right side of the paper to your first pinch; again, just a pinch). This gives you $d_r=1/3-\varepsilon/2$, thus, a better approximation!
Now, repeat this procedure on the left. On the left part you now have $2/3+\varepsilon/2$. Take the left side of the paper to the second pinch to obtain a second approximation of $d_l = 1/3+\varepsilon/4$. Note that, after two pinches, you have reduced your initial error to a quarter!
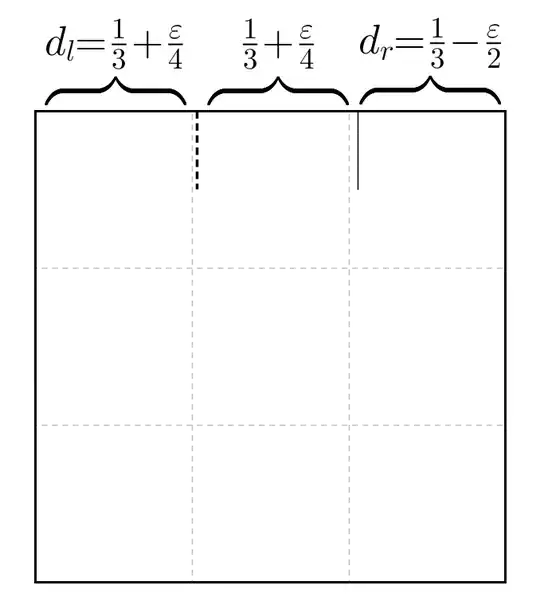
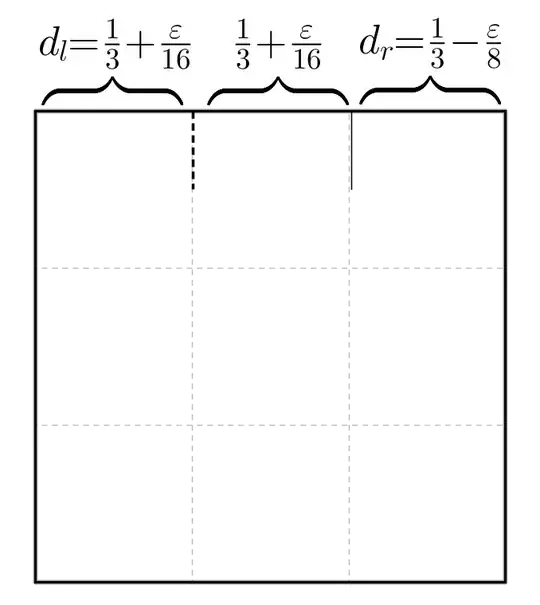
If your initial guess was accurate enough, you will not need to continue more. But, if you need more precission, you just have to repeat the process a couple of times more. For instance, an initial error of $\varepsilon=1$cm reduces to less than 1mm (0.0625mm) after repeating the iteration twice.
- 5,107
-
Could you please tell me what program you used for expressing the length? Thanks in advance. – user143993 Oct 27 '18 at 13:02
-
- Fold bottom to middle, do not crease!
- Fold top to bottom,
- Push bottom into middle,
- Flatten paper gently,
- Crease bottom,
- Crease top.
- 3,401
- 219
A non-mathematical but quick way (which I used when I had to mail hundreds of letters years ago): Bend the paper in the Z-shape as you would want it to fold but without creasing yet, gently push the edges (top of paper and 2/3rds down on the left, 1/3rd down and bottom on the right) together so the edges align automatically, while at the same time making the pile flatter, and finally press the edges down to create the folding. You can do that with 10 sheets simultaneously and still get reasonable results.
- 301
I love the geometrical solutions! That said, there is a trick for more accurate estimation. The trick is not to try to judge 1/3 of the whole sheet but to try to judge 1/2 of the remaining sheet while you are doing the first fold. In other words, as you fold the bottom 1/3 of the sheet upwards, the edge that you are moving upwards approaches the exact middle of the remaining 2/3 of the sheet. For me, this is easy enough to judge, and results in folds accurate to within a couple of millimeters.
- 61
-
That's the solution I described in my comment above. It isn't "mathematical", but it's good enough to solve the problem which motivated the question. – keshlam Apr 07 '14 at 02:06
I don't understand the problem.
You say in your question that you want to "put[...] an A4 letter in a[n] oblong envelope", so what you appear to have is an A4 paper and an envelope. While you don't want to use additional tools, like a ruler, why don't you simply
fold the paper to a bit less than the height of the envelope
? Like this:
Since you know the height of the envelope (which is printed on the packaging when you buy them) you can, if you want to be exact, eyeball 10 mm (for a C5/6 envelope) or 14 mm (for a C6/5 envelope) off the height of the envelope. Eyeballing such a short length is much easier than eyeballing a third of the paper height, and I can do it just as exactly as I can fold a paper according to the instructions in the other answers – which, you may note, don't lead to exact results when you use real paper and real hands instead of maths (see for example the comment by Henk Langeveld under the accepted answer).
-
No, this is not what I meant: no tools for measurement or as you call it "eyeballing" the envelope, but I appreciate you answer and upvoted it! Thanks. – Nicky Hekster Nov 25 '20 at 16:37
5-Fold Technique: Accurate to ~ 1mm (If you can fold in half accurately)
Bend the paper in half, top to bottom, making crease #1 at the center on one edge of the paper.
Bend top down to fit in crease #1 to make crease #2 (1/4 distance from the top).
Reverse paper (back face), bend so crease #1 and crease #2 align and make crease #3 halfway between them.
Reverse paper (original face), bend so that crease #3 fits into crease #2. Make crease #4 halfway between them.
Bend so that crease #3 fits into crease #4. Make crease #5 halfway between them.
Fold bottom to meet (approximately) 1/3 of the way between crease #5 and #4 (closer to #5).
Summary - Final order of creases: bottom, 1, 3, 5, 4, 2, top
top + bottom = 1
top + 1 = 2
1 + 2 = 3 (fold backwards)
3 + 2 = 4
3 + 4 = 5
Does not produce an exact solution but usually does better than guessing the first fold.
- Roll the paper into a tube.
- Allow an overlap to develop that looks right.
- Carefully flatten the tube adjusting the overlap as necessary.
- 585
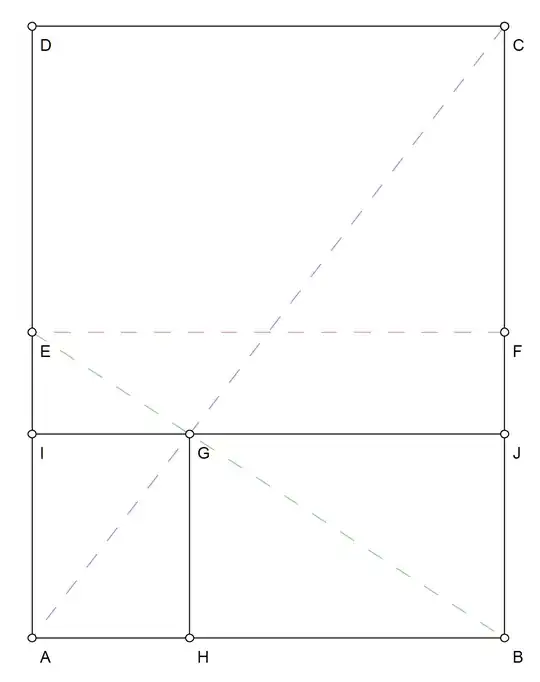
This is a slight variation of the method of Egor Skriptunoff that works for paper of any aspect ratio, not just A4, and so is of use for our non-Continental readers. It uses the solution to the crossed ladders problem, and requires one more fold than Egor's method but fewer than the method of Hagen von Eitzen which also works for any aspect ratio.
- Fold the paper in half along the long side (constructing segment $EF$ in the diagram below, connecting the midpoints of $AD$ and $BC$).
- Fold the paper along the segment $BE$.
- Fold the paper along segment $AC$.
One can show that $GH = \frac{1}{3}AD$, so folding the paper along segment $IJ$ (and then either folding again at the crease, or folding along the segment $DF$ to get another intersection point) will produce the desired fold into thirds.
If the ratio $AB/AD = \sqrt{2}$ as in A4 paper, then we have $AC \bot BE$ (the converse is also true) allowing the omission of steps 1 and 2 that construct $BE$, and we can proceed as in Egor's solution.
- 566

scrlttr2environment as shown here. – Martin Thoma Apr 02 '14 at 14:40