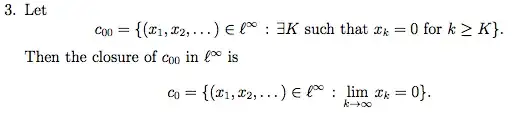Closure of a particular set, $c_{00}$.

Question

I have been learning the concept of closure in metric spaces and all has made sense so far. However, I have come across a particular example that is troubling me in terms of extracting the possible limit points. The example reads as

enter image description here

Thank you in advanced for you help.

Can you be more precise with where the trouble lies? I would suggest a) show that $c_0$ is a closed subspace of $\ell^\infty$, and b) for all $x\in c_0$ find a sequence in $c_{00}$ converging to $x$. — Daniel Fischer, Apr 01 '14 at 13:10
Is that sufficient ? a seq in $c_{00}$ might have a limit outside $c_0$. — DiffeoR, Apr 01 '14 at 13:23
Sorry, my question lies in why the closure is given by what it is, and how it was concluded. — Gustavo Louis G. Montańo, Apr 02 '14 at 01:37

score 2 · Answer 1 · answered Apr 01 '14 at 13:20

To show that the closure of $c_{00}$ is $c_0$ you need to do precisely what Daniel suggests.

a) $c_0$ is closed: Indeed let $(x^n) \subset c_0$ be a sequence (of sequences, each indexed in the following way: $(x_i^n)_{i=1}^{\infty}$) converging to some $x \in l^{\infty}$. We must show that in fact $x \in c_0$. So we must show that $\lim_{i \rightarrow \infty} x_i$ exists. To do this, define $c_n:= \lim_{i \rightarrow \infty} x_i^n$, and show that the sequence $(c_n)$ is Cauchy, using the convergence of $(x_n)$ in the supremum norm. This shows that $(c_n)$ has a limit, $c$. You should then be able to use a simple triangle inequality argument to show that in fact $\lim_{i \rightarrow \infty} x_i = c$.

b) Let $x \in c_{0}$. We must show we can find a sequence $(x^n)$ of $c_{00}$-elements converging in the supremum norm to $x$. You can use the sequence $x_i^n:= x_i$ for $i \leq n$ and $x_i^n:= 0$ for $i>n$.

DiffeoR · Answer 2 · 2014-04-01T13:38:18.007

Consider a point in $c_0$ that is $x = (x_1, x_2, \dots )$ s.t. $x_n \rightarrow 0$. It is the limit of

$Y_1 = (x_1, 0, 0, \dots)$

$Y_2 = (x_1, x_2, 0, 0, \dots)$

$\dots$

Check : $Y_N \rightarrow x$ in $l^\infty$ norm.

So $c_0 \subset \overline{c_{00}}$ under $l^{\infty}$ norm.

Is one side of the proof.

For the other part consider an element $X = (x_1, x_2, \dots)$ in $\overline{c_{00}}$.

Now for given any $\epsilon > 0$ there exists a $X_\epsilon = (x_1^{\epsilon}, x_2^{\epsilon}, \dots )$ s.t. $$ \|X - X_\epsilon\|_\infty < \epsilon$$ because $X_\epsilon$ is in $c_{00}$, n > $n_\epsilon$ all the $x_n^\epsilon = 0$, which amounts to saying :

for all $n > n_\epsilon$ we have $$|x_n| < \epsilon$$

We can choose smaller $\epsilon$ and a larger $n_\epsilon$ in the same fashion every time. Thus seeing that indeed the $x_n \rightarrow 0$.

Closedness of $c_0$ becomes unnecessary in this case. You have $\overline{c_{00}} \subset c_0$ here thus combining both the parts.

$$c_0 = \overline{c_{00}}$$ in $l^\infty$.

Closure of a particular set, $c_{00}$.

2 Answers2

Linked