My attempt at the solution (using $<r,\phi,z>$)
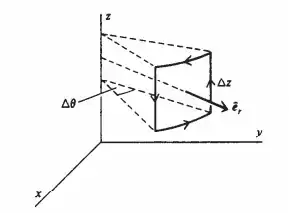
First consider the curve of constant r, provided above. For $C_1$ and $C_3$, we have:
$\int_{C_1} F\cdot \hat{t} = -F_\phi (r,\phi, z + \Delta z/2)(r + \Delta r/2)\Delta \phi$
$\int_{C_3} F\cdot \hat{t} = F_\phi (r,\phi, z - \Delta z/2)(r - \Delta r/2)\Delta \phi$
Thus, knowing the change in surface for constant r is $\delta S_r = r \delta \phi \delta z$
\begin{align*} \frac{1}{\Delta S}\int_{C_1 + C_3} F\cdot \hat{t} = -\frac{\Delta \phi}{r \Delta \phi \ \Delta z}[ F_\phi (r,\phi, z + \Delta z/2)(r + \Delta r/2) - F_\phi (r,\phi, z - \Delta z/2)(r - \Delta r/2)] \end{align*}
Which taking the limits for $\Delta \phi, \Delta z \rightarrow 0$, we get
\begin{align*} -\frac{\delta F_\phi}{\delta z}\end{align*}
For $C_2$ and $C_4$:
$\int_{C_2} F\cdot \hat{t} = F_z (r,\phi + \Delta \phi/2, z)\Delta z$
$\int_{C_4} F\cdot \hat{t} = F_z (r,\phi - \Delta \phi/2, z)\Delta z$
Thus,
\begin{align*} \frac{1}{\Delta S}\int_{C_2 + C_4} F\cdot \hat{t} = \frac{\Delta \phi}{r \Delta \phi \ \Delta z}[F_z(r,\phi + \Delta \phi/2, z) - F_z(r,\phi - \Delta \phi/2, z)] \end{align*}
Which taking the limits for $\Delta \phi, \Delta z \rightarrow 0$, we get
\begin{align*} \frac{1}{r} \frac{\delta F_z}{\delta \phi}\end{align*}
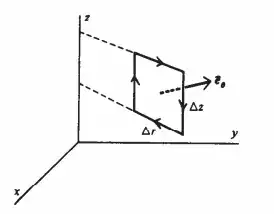
First consider the curve of constant $\phi$, provided above. For $C_1$ and $C_3$, we have:
$\int_{C_1} F\cdot \hat{t} = F_r (r,\phi, z + \Delta z/2)\Delta r$
$\int_{C_3} F\cdot \hat{t} = -F_r (r,\phi, z - \Delta z/2)\Delta r$
Change in surface for constant $\phi$ is $\delta S_r = r \phi \delta z$
\begin{align*} \frac{1}{\Delta S}\int_{C_1 + C_3} F\cdot \hat{t} = \frac{\Delta r}{\Delta r \ \Delta z}[F_r (r,\phi, z + \Delta z/2) - F_r (r,\phi, z - \Delta z/2)] \end{align*}
Which taking the limits for $\Delta r, \Delta z \rightarrow 0$, we get
\begin{align*} \frac{\delta F_r}{\delta z}\end{align*}
For $C_2$ and $C_4$:
$\int_{C_2} F\cdot \hat{t} = -F_z (r + \Delta r/2, \phi, z)\Delta z$
$\int_{C_4} F\cdot \hat{t} = F_z (r - \Delta r/2, \phi, z)\Delta z$
Thus,
\begin{align*} \frac{1}{\Delta S}\int_{C_2 + C_4} F\cdot \hat{t} = -\frac{\Delta z}{\Delta r \ \Delta z}[F_z(r + \Delta r/2, \phi, z)-F_z (r - \Delta r/2, \phi, z)] \end{align*}
Which taking the limits for $\Delta r, \Delta z \rightarrow 0$, we get
\begin{align*} \frac{\delta F_z}{\delta r}\end{align*}
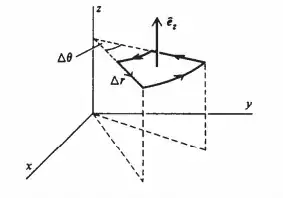
The derivation for the final curve, of constant $z$, shown above, can be found in Schey's "Div Grad Curl and All That", but it follows the same procedure as above.
The result for the curve of constant $z$ is
\begin{align*} (\nabla \times F)_z =\frac{1}{r}\frac{\delta}{\delta r} (rF_\phi) - \frac{1}{r} \frac{\delta F_r}{\delta \phi} \end{align*}
Combining the results of the above, we reach
\begin{align*} \nabla\times\vec{F} = (\frac{1}{r} \frac{\delta F_z}{\delta \phi} - \frac{\delta F_\phi}{\delta z}) \hat{r} + (\frac{\delta F_r}{\delta z} - \frac{\delta F_z}{\delta r})\hat{\phi} + \frac{1}{r}(\frac{\delta(r F_\phi)}{\delta r} - \frac{\delta F_r}{\delta \phi} )\hat{z}\end{align*}


