function whose limit does not exist but the integral of that function equals 1

Question

Is there a function whose limit does not exist as x approaches infinity but the integral of that function from negative infinity to positive infinity is equal to 1?

Answer 1

I think the general principle behind @heropup's example is the following rather simple idea:

That idea even can be exhausted to create a smooth function whos integral equals one though its limit at infinity does not exist (pasting smooth bump functions rather than merely continuous peeks).

Answer 2

An example of a continuous and differentiable function $f : \mathbb R \to \mathbb R^+$ such that $\lim_{x \to \infty} f(x)$ does not exist, but $\int_{x=0}^\infty f(x) \, dx < \infty$, is $$f(x) = \sum_{k=1}^\infty \frac{1}{1+k^4 (x-k^2)^2}.$$ Clearly, $0 < f(x) < \infty$ for all $x$ (convergence is assured by a simple comparison test). It is intuitive that $\displaystyle \lim_{x \to \infty} f(x)$ does not exist: details of a formal proof is left to the reader. The idea is that $f(n^2) > 1$ for each $n \in \mathbb Z^+$, but $f(x) \to 0$ for sufficiently large $x$ not "close" to a square. Meanwhile, the integral is bounded above by $$\int_{x=0}^\infty \sum_{k=1}^\infty \frac{dx}{1+k^4(x-k^2)^2} = \sum_{k=1}^\infty \frac{\pi + 2 \tan^{-1} k^4}{2k^2} < \pi \sum_{k=1}^\infty \frac{1}{k^2} = \frac{\pi^3}{6}.$$

Answer 3

Yes, take your favorite continuous function with the required integral. Then change $f(n)$ to $1$ for all $n \in \Bbb N$ Changing those points does not change the integral. For a specific example, $$f(x)=\begin {cases} 0& x \le 0 \\1&x \in \Bbb N \\ \exp(-x)& x \gt 0 \wedge x \not \in \Bbb N \end {cases}$$

Answer 4

If you allow discontinuities, then you could take your favorite function with integral 1, and add discontinuities at each natural number. The integral doesn't change since the set of discontinuities has measure zero, but the limit doesn't exist.

Answer 5

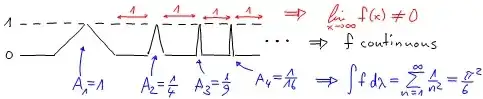
Let $f$ be the function given by $$ f(t)=\begin{cases}2^{n+1}(t-n),&\ t\in[n,n+1/2^{n+1})\\ 3-2^{n+1}(t-n),&\ t\in[n+1/2^{n+1},n+1/2^n]\\ 0,&\ \text{ otherwise }\end{cases} $$

(if you don't want to bother with the computations, at the beginning of each interval it consists of a triangle of height 2 and base $1/2^n$, so its area is $1/2^n$. Over the rest of each interval, the function is zero. The integral will be the sum of the areas of these triangles, which add to one)

This function is continuous. It's limit at infinity does not exist, because it achieves all values from zero to two between any two consecutive integers. And $$ \int_0^\infty f(t)dt=\sum_{n=1}^\infty\int_n^{n+1}f(t)dt=\sum_{n=1}^\infty\int_0^1f(t+n)dt\\ =\sum_{n=1}^\infty\int_0^{1/2^{n+1}}2^{n+1}t\,dt+\int_{1/2^{n+1}}^{1/2^{n}}(3-2^{n+1}t)\,dt\\ =\sum_{n=1}^\infty\frac{2^{n}}{2^{2n+2}}+\frac3{2^{n+1}}-2^{n}\left(\frac1{2^{2n}}-\frac1{2^{2n+2}} \right)\\ =\sum_{n=1}^\infty\frac1{2^n}=1 $$

If you want to give up absolute convergence of the integral, you can even get $f$ to be infinitely differentiable, as in Random Variable's example: $f(x)=\sqrt{2/\pi}\,\sin(t^2)$ (if over the whole line, otherwise one multiplies by 2).