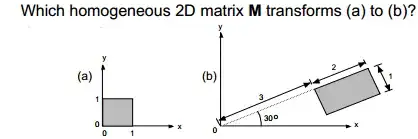
So from what I understand from this picture, the box is stretched to twice its width. And it is then flipped from the x-axis. And then it is rotated 30 degrees anticlockwise.
So these three transformations are Scaling, then Reflection then Rotation.
How am I supposed to go about answering this problem. Also, it says which homogenous 2d matrix, this is confusing for me because when you convert cartesian coordinates to homogenous coordinates, you are going from 2d - 3d. This question is saying homogenous but it is a purely 2d transformation, I find this confusing.
Any help would be appreciated.
EDIT: Final matrices:
The scaling matrix is... $$\begin{bmatrix}2& 0& 0\\ 0& 1 & 0\\0& 0 & 1\end{bmatrix}$$ The translation matrix is... $$\begin{bmatrix}1& 0& 3\\ 0& 1 & -1\\0& 0 & 1\end{bmatrix}$$ And the Rotation matrix is...$$\begin{bmatrix}\cos(30) & -\sin(30) & 0\\ \sin(30) & \cos(30) & 0\\ 0 & 0 & 1 \end{bmatrix}$$
Is that right? Now you simply matrix multiply?