1

I question a new from my other question because this issue didn't occur until presently.

I understand $0<|x-c|<\delta \implies |f(x)-f(c)|<\epsilon $
and $x = c \implies |f(c)-f(c)| = 0 <\epsilon .$

but I still don't understand how $\color{red}{(I)} \; ... 0 \le |x - c|...$
$\color{red}{\implies (III)} \; ... 0 < |x - c|...$

Doesn't this contradict $a \le b \not \implies \Leftarrow a < b$ ?

dafinguzman wrote under that answer "Every human dies" implies that "Every woman dies".
It doesn't mean that "a is human ⟹ a is woman" (I am certainly not one)."

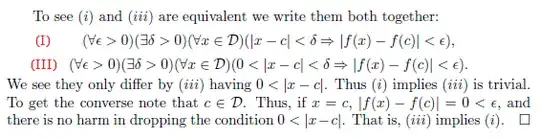
enter image description here

@HagenvonEitzen Can you please demystify what are P, Q, R, S in your answer?

Community
  • 1
  • It is not true that $\text{Your }\color{red}{(I)}\implies \text{Your }\color{red}{(III)}$. – Git Gud Mar 13 '14 at 15:02
  • (III) just makes the additional assumption $|x-c|\neq 0 \Leftrightarrow x\neq c$, thus it is "stronger" than (I). You may not pull expressions out of context like you did. – AlexR Mar 13 '14 at 15:06
  • 1
    @GitGud When I wrote my comment, I had the $(I)$ and $(III)$ from the bottom part before my eyes, for these, we have $(I)\implies (III)$, not for the ones at the top. – Daniel Fischer Mar 13 '14 at 15:07
  • The whole mess stems from the fact that most people define continuity in terms of limits, instead of the other way round. Continuity is the primary notion, and limits are just for "exception handling". – Christian Blatter May 11 '14 at 12:28

2 Answers2

2

(I) implies (III) because the implication in (III) is certainly weaker than the implication in (I). It is not that $0 \le \mid x-c \mid \implies 0 \lt \mid x-c \mid$ (which would be wrong), it is that $(0 \le \mid x-c \mid \implies \dots) \implies (0 \lt \mid x-c \mid \implies \dots)$.

Rephrasing might help:

If $A \implies X$ is true and $B \implies X$ is true then (trivially) $B \implies X$ is true. Here $A$ stands for $0 = \mid x-c \mid$ and $B$ stands for $0 \lt \mid x-c \mid$.

vuur
  • 1,264
1

Assume $P\to Q$. Then $Q\to R$ implies $P\to R$: $$P\to Q\\\underline{Q\to R}\\P\to R $$ You seem to confuse this with $$P\to Q\\\underline{S\to P}\\S\to Q $$

Hagen von Eitzen
  • 382,479