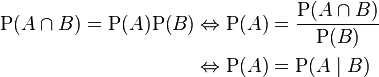4

I know there are two ways to say event $a$ and $b$ are independent:

  • $P(a)P(b)=P(a\cap b)$
  • $P(a\mid b)=P(a)$

and I can derive one from the other with the Bayes Formula $P(a|b)=P(a\cap b)/P(b)$.
My question is: Of the two equations above, which is the definition from which the other equation is proven?

Oren Milman
  • 521
  • 6
  • 11
zhangxaochen
  • 345
  • Interesting question! But, doesn`t this depend on the case, when you are using the formula? Whats do you want to achieve with this question? – Carol.Kar Mar 13 '14 at 08:51

3 Answers3

4

After a few days searching, I find it's clearly explained in the wiki pages:

Two events A and B are independent if and only if their joint probability equals the product of their probabilities:

$P(A∩B)=P(A)P(B) $

Why this defines independence is made clear by rewriting with conditional probabilities: conditional probabilities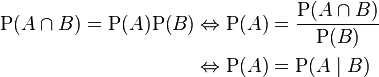

Although the derived expressions may seem more intuitive, they are not the preferred definition, as the conditional probabilities may be undefined if $P(A)$ or $P(B)$ are 0. Furthermore, the preferred definition makes clear by symmetry that when $A$ is independent of $B$, $B$ is also independent of $A$.

zhangxaochen
  • 345
1

If my primitive you mean immediately apparent, and obvious I would say $$P(a)*P(b)=P(ab)$$ but this might be considered subjective, although in practice, that equation is where almost all probability classes start. It is quite intuitively obvious, although to a prodigy Baye's theorem might be "obvious" as well.

Guy
  • 9,055
  • 1
  • 30
  • 58
  • 1
    To me, the intuitive definition of independence is saying "the probability of $a$ does not change if $b$ occurs or not", which directly means $P(a|b)=P(a)$. If I think of real life random events, I normally use that to determine whether events are independent, and then use Bayes formula to get $P(a)P(b)=P(ab)$. But in probability theory, it is common to define independence by $P(a)P(b)=P(ab)$; that's a simpler formula mathematically and it is easier to build from that. – JiK Mar 13 '14 at 08:56
  • @JiK yes it is common to define independence by $P(a)P(b) =P(ab)$ which is intuitive too. But $P(a|b)=P(a)$ is intuitive as well. It is through this combined intuition that you understand Baye's theorem. You do not need to take it for granted. – Guy Mar 13 '14 at 10:01
0

I've most often seen $P(A\cap B) = P(A)P(B)$ as the definition of independence, and for independent events $A,B$, $P(A|B)=P(A)$ as a theorem that one proves using the previous definition. So in that sense $P(A\cap B) = P(A)P(B)$ is as "primitive" as it gets.

crf
  • 5,679