How to intuivitely see that $e^{i \pi}+1=0$ is true?

Question

Gauss is reported to have said that if Euler's formula $e^{i \pi} + 1 = 0\,\!$ "was not immediately apparent to a student upon being told it, that student would never be a first-class mathematician."

How is someone supposed to see that this is true?

Answer 1

$e^{i \theta} = \cos \theta + i \sin \theta$

Thus, on the complex plane, it makes the equation of a circle, with $\theta$ mapping to a point on the circle with angle $\theta$.

With $\theta = \pi$, that maps to the point of the circle on the negative real axis, namely the point $-1$.

Answer 2

Another approach is like this. Supposing that $f(x) = \cos x + i\sin x$ for all real $x$ we get $f'(x) = -\sin x + i\cos x = if(x)$. We treat $i$ as just a constant with property $i^{2} = 1$. Now put $g(x) = e^{-ix}f(x)$ so that $g'(x) = e^{-ix}if(x) -ie^{-ix}f(x) = 0$ so that $g(x)$ is a constant and hence $g(x) = g(0) = f(0) = 1$ and therefore $f(x) = e^{ix}$. putting $x = \pi$ we get $e^{i\pi} = f(\pi) = -1$.

The above derivation rests on the assumption that the symbol $e^{-ix}$ can be treated in a manner like $e^{kx}$ where $k$ is real and follows same rules of differentiation. This is something which needs a proper justification.

---

Update: After the comments user92774 I think I should put the above argument into a more intuitive manner. So let's start with $f(x) = \cos x + i\sin x$. This is a very common expression if one knows about polar form of a complex number. By differentiating it we get $f'(x) = if(x)$ so that the derivative is a constant multiple of the original function. From the existing knowledge of exponential/logarithm function we know that the function $e^{kx}$ possesses this property that $\{e^{kx}\}' = ke^{kx}$ for real constant $k$. It is now easy to compare this with $f(x)$ and extend our imagination and put $k = i$ and set $f(x) = e^{ix}$. This leads to a natural definition of $e^{ix}$ as $f(x)$ and $e^{x + iy} = e^{x}f(y)$ thereby extending the domain of exponential functions to entire complex plane.

Answer 3

As I mentioned in the comments to another answer here, you need a "special kind of intuition about the exponential function". I believe I might have thought of one. It uses physical reasoning.

The exponential function, $e^x$, is a fixed point of the derivative. That is,

$$\frac{d}{dx} e^x = e^x$$.

Assume it's also true for $x = it$, $t$ rael. By the chain rule, $\frac{d}{dt} e^{it} = ie^{it}$. You can think of this as "position/time", i.e. velocity in the plane. Differentiating it again gives acceleration. The acceleration is $-e^{it}$. This is $i$ times the velocity, therefore it lies at right angles to it. So at every point in time, the acceleration is always at right angles to the velocity, from which you might be able to intuit that it moves on a circular path.

You can show that $|e^{it}| = 1$ by taking the conjugate $\overline{e^{it}} = e^{-it}$ (which follows from the derivative equation by $\frac{d}{dt} \overline{e^{it}} = \overline{\frac{d}{dt} e^{it}} = \overline{ie^{it}} = \overline{i} \overline{e^{it}} = -i \overline{e^{it}}$, so $\overline{e^{it}}$ satisfies $f'(t) = -i f(t)$, which is the same equation as $e^{-it}$ satisfies. Noting that this differential equation is first-order linear and $e^0 = 1$, the equality $\overline{e^{it}} = e^{-it}$ is obtained.) and multiplying to get the square of the absolute value, $e^{it} e^{-it} = e^{it + -it} = e^0 = 1$. This alone shows the motion is on a circle, but the constant magnitude of velocity and acceleration show that it is circular orbital motion about the origin, and not, say, chaotically bouncing back and forth along the circle or some other weirdness like that.

Then it's not unreasonable to imagine that $t$ is an angle, and $e^{i \pi} = -1$, from which the formula follows. Actually, from the knowledge of the constant and equal magnitude of the velocity and acceleration and the fact the acceleration is always at right angles to the velocity, you can use physical reasoning to arrive at Euler's formula directly, i.e. $e^{it} = \cos(t) + i \sin(t)$.

Answer 4

We have that $\lim_{n \to \infty} (1 + \frac{i \pi}{n})^n = -1$. As $n \to \infty$, $\sqrt{1 + (\frac{\pi}{n})^2} \to 1$, so the first $(1 + \frac{i \pi}{n})$ has magnitude $1$ and further multiplications of it by itself won't change its magnitude.

Furthermore, we have that $\lim_{x \to 0} \tan x = x$, so the argument of $(1 + \frac{i \pi}{n})$ is $\frac{\pi}{n}$ as $n \to \infty$. Since we multiply $n$ times, the argument is $\pi$.

So $e^{i \pi}$ is a complex number with magnitude $1$ and argument $\pi$, namely $-1$.

Personally I find this to be very intuitive, but it won't be something you can figure out without some rudimentary knowledge of complex numbers.

Answer 5

You can easily show geometrically, that if rotation+scaling is a multiplication, if the y axis is mapped onto $i$. So scaling rotation of r,a * R,A gives Rr, a+A. One can easily suppose a is an exponent, but the jump to radians and e needs series analysis. It is possible to show that $i^2=-1$.

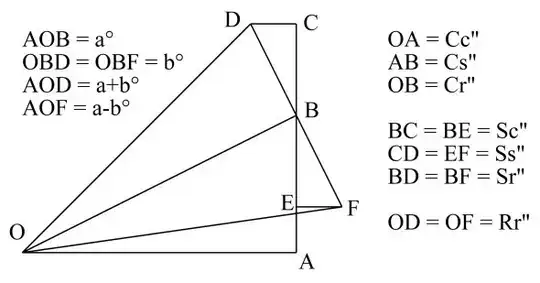
In the diagram, we wish to multiply R cis(A) by r cis(a), demonstrating that rotation and scaling comes out as complex multiplication.

We start with the triangle OAB being r cis(a), scaled by C, so OA is Cc, OB is Cs, and OB is Cr. Extend AB to C, so that BCD is a copy of OAB, scaled by S: ie BD=Sc, CD=Ss, and BD is Sr. The triangle OBD is a copy of C:S:R, scaled by a factor of r. The side OB is rC, the side BD is rS, and OD is rR.

We have now shown that OD is the point at rR cis(a+A).

One can calculate the point D as $Cc-Ss + i(Cs + sS)$. But the product of C+iS and c+is is $Cc+Ssi^2 + i(Cs+sC)$. Since these are equal, we get $i^2=-1$.

This is a geometric proof of the argand diagram.

While we have shown that complex multiplication corresponds to dialation and rotation, it is not immediately obvious that this is $e^{i\theta}$. One has to resort to the expansion of series of cosine and sine, and exponential, to see this is the case.