Consider the set $\{u_{1}, u_{2}, \ldots, u_{n}\}$ of points on the spere in $\mathbb{R}^{3}$ (i. e. $||u_{i}|| = 1$) and their convex hull C = $Hull(u_{1}, \ldots, u_{n})$. It's obvious that each $u_{i}$ is the vertex of $C$. Suppose that $C$ is simplicial, i. e. each its facet is a triangle.
Let us consider the n-tuple of real numbers $(h_{1}, \ldots, h_{n}) \in \mathbb{R}^{n}$ construct a polyhedron $C(h_{1}, \ldots, h_{n})$ that has edges $v_{i} = h_{i} u_{i}$ and the same incidence structure as $C$. (It can be done by dividing $C$ into tetrahedrons $T(O, u_{i_{1}}, u_{i_{2}}, u_{i_{3}})$) and then constructing $C(h_{1}, \ldots, h_{n})$ as the union of $T(O, v_{i_{1}}, v_{i_{2}}, v_{i_{3}})$).
Now let us check whether the $C(h_{1}, \ldots, h_{n})$ is convex or not. All $u_{i}$ are considered to be fixed, and $h_{i}$ are variables.
Mehlhorn et al. have proved the following theorem for polyhedron convexity:
Theorem 6. Let $\mathfrak{F}$ be a simplicial $(d − 1)$-dimensional surface without boundary in $\mathbb{R}^{d}$ that is consistently oriented, let $o$ be center of gravity of all the vertices of surface $\mathfrak{F}$ and let $p$ be the center of gravity of some facet of $\mathfrak{F}$ . Then $\mathfrak{F}$ is the surface of a convex body iff
- $\mathfrak{F}$ is locally convex at all its ridges,
- $o$ is on the negative side of all its facets, and
- the ray emanating from $o$ and passing through $p$ intersects only the facet containing $p$.
In our case the situation is simple: since all $u_{i}$ are fixed, we do not need to check conditions 2 and 3 (since the polyhedron is star-shaped). Condition 1 means that dihedral angle at each edge $(u_{1}, u_{2})$ is less than $\pi$, or that the signed volume of tetrahedron $V(v_{1}, v_{2}, v_{3}, v_{4})$ has the same sign as $V(u_{1}, u_{2}, u_{3}, u_{4})$:
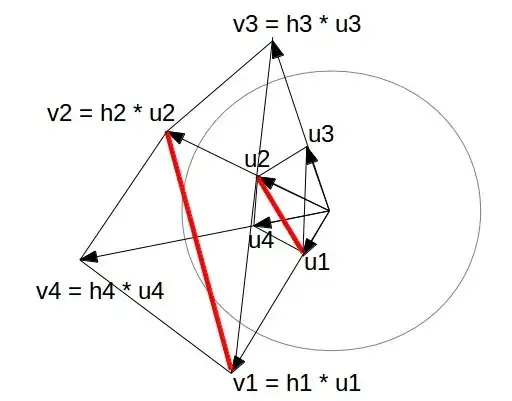
In terms of our variables this condition can be formulated as follows:
$$ \left| \begin{array}{cccc} h_{1} & u_{1x} & u_{1y} & u_{1z} \\ h_{2} & u_{2x} & u_{2y} & u_{2z} \\ h_{3} & u_{3x} & u_{3y} & u_{3z} \\ h_{4} & u_{4x} & u_{4y} & u_{4z} \\ \end{array} \right| \left| \begin{array}{cccc} 1 & u_{1x} & u_{1y} & u_{1z} \\ 1 & u_{2x} & u_{2y} & u_{2z} \\ 1 & u_{3x} & u_{3y} & u_{3z} \\ 1 & u_{4x} & u_{4y} & u_{4z} \\ \end{array} \right| \geq 0 $$
This condition is linear condition in terms of variables $h_{1}, h_{2}, h_{3}, h_{4}$
The theorem mentioned above states that each edge should be checked. But on e case makes me doubt. If the vertex has degree 3 (i. e. it has 3 incident edges) then conditions for all its incident edges are equal, because the tetrahedron is the same for all them:
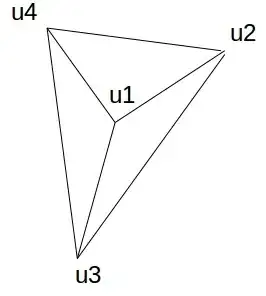
So we can avoid checking all 3 edges and check only 1 edge for vertex $u_{1}$.
Can it be done for the vertexes of degree higher than 3? Is it possible to reduce the number of conditions from $ord(v)$ to $ord(v) - 2$ ?