Computing $\int{2\sec^3xdx}$

Question

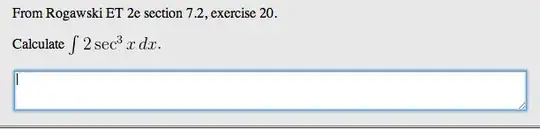
enter image description here

I attempted to solve this problem by taking the two out of the integral. Then, I changed $\sec^3(x)$ to $\frac{1}{\cos^2(x)\cos(x)}$ and attempted to replace $\cos^2(x)$ with $1 - \sin^2(x)$.

However, I do not know where to go from here. Any insight, hints, tips, or answers would be fantastic.

Thank you for your time.

$\sec^2{x} = (d/dx) \tan{x}$. Then use integration by parts. — Ron Gordon, Feb 24 '14 at 22:51
consider splitting $sec^3x$ to $secxsec^2x$ then employ integration by parts as suggested by ron, note which terms you want to differentiate and integrate depending on known results you should have. — WhizKid, Feb 24 '14 at 23:00
Thank you very much Ron and Whizkid, that helped tremendously — zackymo21, Feb 24 '14 at 23:03
Most calculus textbooks show step-by-step how to integrate the odd powers of $\sec x$. Look it up in the section on trigonometric integrals. — LeoTheKub, Feb 25 '14 at 00:16

Steven Van Geluwe · Answer 1 · 2014-08-07T08:34:34.947

Use the fact that $\sec^2x=(\tan x)'$ and partial integrate: $$ 2\int{\sec^3(x)dx}=2\int(\tan x)'\sec x dx=2\tan x\sec x -2\int \frac{\sin^2x}{\cos^3x}dx$$ In order to solve the last integral, use the formula $\sin^2x=1-\cos^2x$ and split the integral in two parts:
$$=2\tan x\sec x +2\int \frac{1}{\cos x}dx-2\int \frac{1}{\cos^3 x}dx$$ $$=2\tan x\sec x +2\ln(\sec x+\tan x)-2\int \sec^3 x dx$$ Bring the integral $\int{\sec^3x dx}$ to the other side of the equation: $$4\int{\sec^3(x)dx}=2\tan x\sec x +2\ln(\sec x+\tan x)$$ In conclusion: $$\int{\sec^3(x)dx}=\frac{1}{2}\tan x\sec x +\frac{1}{2}\ln(\sec x+\tan x)$$

Computing $\int{2\sec^3xdx}$

1 Answers1