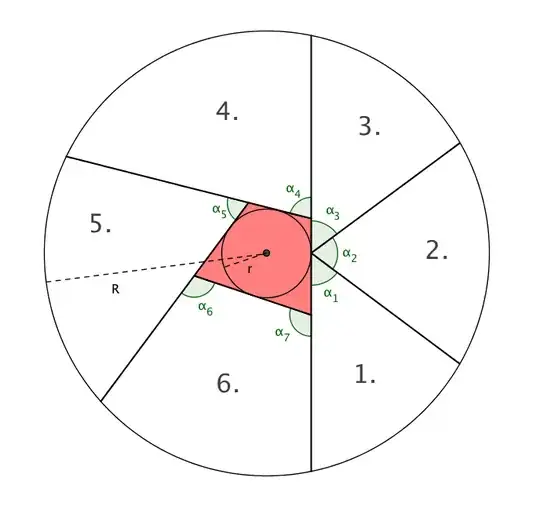
Too long for comment but may give some useful ideas for setting up the integrals in spherical coordinates (cylindrical may be slightly simpler):
Make the first cut into the sphere $x^2+y^2+z^2=R^2 \iff \rho=R$ along the plane $x=r \iff \rho=r\sec(\theta)\csc(\phi)$. Letting $\theta$ vary over a fixed symmetric interval, solve for $\phi$ when the plane and sphere meet to get
$$r\sec(\theta)\csc(\phi)=R \implies \sin(\phi) = \frac rR \sec(\theta)$$
In the plane $z=0$, when $\phi=\frac\pi2$, we have
$$r\sec(\theta)=R \implies \cos(\theta) = \frac rR$$
Hence the volume of the first half is given by the integral(s)
$$\begin{align*}
V_1+V_2+V_3&=\int_{-\cos^{-1}\left(\frac rR\right)}^{\cos^{-1}\left(\frac rR\right)} \int_{\sin^{-1}\left(\frac rR \sec(\theta)\right)}^{\pi - \sin^{-1}\left(\frac rR \sec(\theta)\right)} \int_{r\sec(\theta)\csc(\phi)}^R \rho^2 \sin(\phi)\,d\rho\,d\phi\,d\theta\\[1ex]
&= \frac13 \int_{-\cos^{-1}\left(\frac rR\right)}^{\cos^{-1}\left(\frac rR\right)} \int_{\sin^{-1}\left(\frac rR \sec(\theta)\right)}^{\pi - \sin^{-1}\left(\frac rR \sec(\theta)\right)} \left(R^3\sin(\phi)-r^3\sec^3(\theta)\csc^2(\phi)\right)\,d\phi\,d\theta \\[1ex]
&= \frac23 \int_{-\cos^{-1}\left(\frac rR\right)}^{\cos^{-1}\left(\frac rR\right)} \frac{\left(R^2\cos^2(\theta)-r^2\right)^{\frac32}}{\cos^3(\theta)}\,d\theta \\[1ex]
&= \frac{4R^3}3 \int_r^R \frac{\left(\lambda^2-r^2\right)^{\frac32}}{\lambda^3\sqrt{R^2-\lambda^2}} \, d\lambda
\end{align*}$$
which agrees with the spherical cap formula.
To isolate the volume of just the first wedge, it would be convenient to fix the point of tangency of the cut to the core to lie in the planes $x=r$ and $y=0$, and to know $\alpha_1$. Then we can find an equation for the plane representing the cut that forms $V_1,V_2$, $\rho_1 = \frac{r\csc(\phi)}{\cos(\theta)+\tan(\alpha_1)\sin(\theta)}=\frac{r\csc(\phi)}{\sec(\alpha_1)\cos(\theta-\alpha_1)}$.
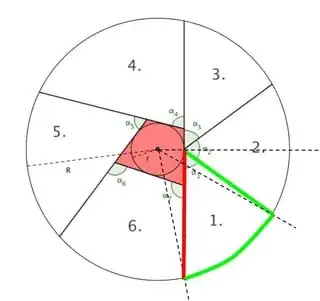
The bounds highlighted in red (part of the very first cut) and green represent the lower and upper limits of $\rho$ - in particular, the green boundary is $\rho=\min\left(\rho_1,R\right)$. The south-southeasternmost ray is $\theta=-\cos^{-1}\left(\frac rR\right)$. Let the other two be given by $\theta=\theta_1$ and $\theta=\theta_2$.
When $\theta\in\left[-\cos^{-1}\left(\frac rR\right),\theta_1\right]$, the integral takes the same the limits for $\phi$ as the integral for the first half.
When $\theta\in[\theta_1,\theta_2]$, we see the cut $\rho_1$ meets the sphere for
$$\frac{r\csc(\phi)}{\sec(\alpha_1)\cos(\theta-\alpha_1)} = R \implies \sin(\phi) = \frac{r\cos(\alpha_1)}{R\cos(\theta-\alpha_1)}$$
We find $\theta_1$ by solving for $\theta$ in the above equation when $\phi=\frac\pi2$:
$$\frac{r}{\sec(\alpha_1)\cos(\theta-\alpha_1)} = R \implies \cos(\theta-\alpha_1) = \frac rR \cos(\alpha_1) \\ \implies \theta_1 = \alpha_1-\cos^{-1}\left(\frac rR \cos(\alpha_1)\right)$$
We find $\theta_2$ by finding where the first cut meets the cut $\rho_1$:
$$r\sec(\theta)\csc(\phi) = \frac{r\csc(\phi)}{\sec(\alpha_1)\cos(\theta-\alpha_1)} \implies \frac{\cos(\theta)}{\cos(\theta-\alpha_1)}=\cos(\alpha_1) \\ \implies \theta_2 = 0$$
Then the integral for $V_1$ has limits
$$\int_{-\cos^{-1}\left(\frac rR\right)}^{\alpha_1-\cos^{-1}\left(\frac rR \cos(\alpha_1)\right)} \int_{\sin^{-1}\left(\frac rR \sec(\theta)\right)}^{\pi-\sin^{-1}\left(\frac rR \sec(\theta)\right)} \int_{r\sec(\theta)\csc(\phi)}^R \\
+ \int_{\alpha_1-\cos^{-1}\left(\frac rR \cos(\alpha_1)\right)}^0 \int_{\sin^{-1}\left(\frac{r\cos(\alpha_1)}{R\cos(\theta-\alpha_1)}\right)}^{\pi-\sin^{-1}\left(\frac{r\cos(\alpha_1)}{R\cos(\theta-\alpha_1)}\right)} \int_{r\sec(\theta)\csc(\phi)}^{\frac{r\csc(\phi)}{\sec(\alpha_1)\cos(\theta-\alpha_1)}}$$