The equation of a line reflected about another line

Question

I need to find the equation of this reflected line:

Answer 1

The General Formula for finding the equation of the line when the line $Ax+By=C$ is reflected at the line $Dx+Ey=F$.

$$y-k=\left(\frac{AE^2-AD^2-2BDE}{BE^2-BD^2+2ADE}\right)(x-h)$$ where $$h=\frac{CD-AF}{BD-AE}$$ $$k=\frac{CE-BF}{AE-BD}$$

Where $(h,k)$ is the intersection of the lines.

If the lines are parallel, the slope becomes:

$$\frac{AE^2-AD^2-2BDE}{BE^2-BD^2+2ADE}=-\frac{A}{B}=-\frac{D}{E}$$

With equation: $$y=-\frac{D}{E}x+\left[\frac{2F}{E}-\frac{AC\left(E^{2}+D^{2}\right)}{ED\left(A^{2}+B^{2}\right)}\right]$$

For horizontal lines $(A,D = 0)$: $$y=\frac{2F}{E}-\frac{C}{B} $$

For vertical lines $(B,E = 0)$: $$x=\frac{2F}{D}-\frac{C}{A} $$

This is easily derived by the use of perpendicular slopes and midpoint formula.

Answer 2

The equation for your reflected line can be constructed using the point-slope form, $y=m(x-x_Q)+y_Q$. The point $(x_Q,y_Q)$ is easily obtained as the intersection of your "mirror" line (the blue one) and the line to be reflected (the solid red one). This leaves the problem of the slope. To get you started, recall that if a line has slope $m$ and is at an angle $\phi$ from the $x$-axis, then $m=\tan\,\phi$. You can try using the sum/difference formulae for the tangent to derive the slope of the reflected line (the dashed red one) from the slopes $k_n$ and $k_m$.

Answer 3

The parametric equation of the blue line is $Z+tr_b$, where $t\in \mathbb R$ and $r_b=(1,k_n)$, the parametric equation of the red line is $Z+tr_r$, where $t\in \mathbb R$ and $r_r=(1,k_m)$. Then the parametric equation of the red dotted line is $Z+tr_d$, where $r_d=(r_1,r_2)$ is symmetric to $r_r$ with respect to $r_b$ and $t\in \mathbb R$. Then $|r_d|=|r_r|$ and $(r_d,r_b)=(r_r,r_b)$. That is $r_1^2+r_2^2=1+k_m^2$ and $r_1+r_2k_n=1+k_nk_m$. Then $(1+k_nk_m-r_2k_n)^2+r_2^2=1+k_m^2$. This is a square equation with respect to $r_2$ and one of its roots is $k_m$. Vieta's formula implies that the other root is $r_2=\frac{k_n^2k_m+2k_n-k_m}{1+k_n^2}$. Then $r_1=1+k_nk_m-k_nr_2$. The canonical equation of the red dotted line is $(y-Y_q)r_1=(x-X_q)r_2$.

Answer 4

I'm going to write a proof of the formula written by William II.

When $l : Ax+By=C$ is reflected at $L : Dx+Ey=F$, the equation of the reflected line $l_r$ is given by $$\begin{cases}p(y-h)=q(x-k)&\text{if $AE\not=BD$} \\\\x=\dfrac{2AF-CD}{AD}&\text{if $B=E=0$} \\\\y=-\dfrac{D}{E}x+\dfrac{2BF-EC}{BE}&\text{if $AE=BD$ and $BE\not=0$}\end{cases}$$ where $$k=\frac{CE-BF}{AE-BD},h=\frac{AF-CD}{AE-BD}$$ $$p=BE^2-BD^2+2ADE$$ $$q=AE^2-AD^2-2BDE$$

Proof :

Case 1 : $AE\not=BD$ and $B\not=0$

The intersection point of $l$ with $L$ is given by $P(k,h)$.

$Q(0,\frac CB)$ is a point on $l$. Let $R(s,t)$ be the reflection point of $Q$.

Since the midpoint of $QR$ is on $L$, we have $$D\times\frac{s}{2}+E\times\frac{\frac CB+t}{2}=F\tag1$$

Since the line $QR$ is perpendicular to $L$, we have $$\frac{-D}{E}\times\frac{t-\frac CB}{s}=-1\tag2$$

Solving the system $(1)(2)$, we have $$s = \frac{2 (B D F - C D E)}{B (D^2 + E^2)},t = \frac{2 B E F + C D^2 - C E^2}{B (D^2 + E^2)}$$

The equation of $l_r$, i.e. $PR$ is given by $$y-h=\frac{t-h}{s-k}(x-k)$$ We have $$\begin{align}\frac{t-h}{s-k}&=\frac{B(D^2+E^2)(AE-BD)(t-h)}{B(D^2+E^2)(AE-BD)(s-k)} \\\\&=\frac{(AE^2-A D^2 - 2 B D E) (BF-C E)}{( BE^2- B D^2 +2 A D E) (B F - C E)} \\\\&=\frac{AE^2-A D^2 - 2 B D E}{BE^2- B D^2 +2 A D E}\end{align}$$

Therefore, we finally get $$(BE^2-BD^2+2ADE)(y-h)=(AE^2-AD^2-2BDE)(x-k)$$ (this works even when $BE^2-BD^2+2ADE=0$)

Case 2 : $AE\not=BD$ and $B=0$

In a similar way as the one in Case 1, we see that the equation of $l_r$ is $$2DE(y-h)=(E^2-D^2)(x-k)$$

Case 3 : If $B=E=0$, then the equation of $l_r$ is $ADx=2AF-CD$.

Case 4 : If $AE=BD$ and $BE\not=0$, then the equation of $l_r$ is $BDx+BEy=2BF-EC$.

Answer 5

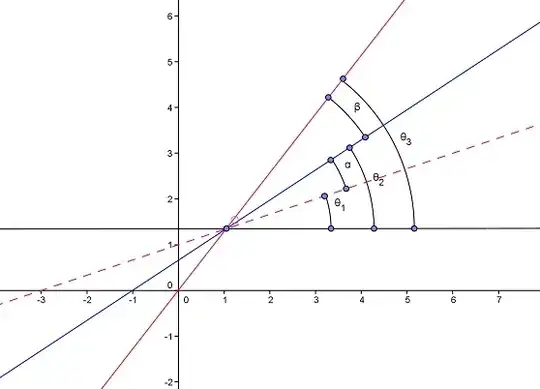
Let's observe picture below. First of all note that $k_1=\tan\theta_1$ ; $k_2=\tan\theta_2$ and $k_3=\tan\theta_3$

Since dashed red line is reflection of the solid red line we may write next equality: $\alpha=\beta$ $\Rightarrow \theta_2-\theta_1=\theta_3-\theta_2$ . Now, if we apply $\tan$ on the both sides we get following: $\tan(\theta_2-\theta_1)=\tan(\theta_3-\theta_2)$ $\Rightarrow \frac{\tan\theta_2-\tan\theta_1}{1+\tan\theta_2\tan\theta_1}=\frac{\tan\theta_3-\tan\theta_2}{1+\tan\theta_3\tan\theta_2}$$\Rightarrow \frac{k_2-k_1}{1+k_2k_1}=\frac{k_3-k_2}{1+k_3k_2}$, so we can find $k_1$ from the last equation. Since $y_1=k_1x_1+C_1$ and we know that point $Z(x_q,y_q)$ belongs to the dashed red line we may write $y_1=k_1x_1+C_1$ and find $C_1$.

Answer 6

Let $l$ be the line $ax+by+c=0$. Let $m$ be the line $dx+ey+f=0$. Let $r$ be the reflection of $m$ in $l$.

When we reflect an equation in $l$, to get the new equation, simply replace each $x$ with $x-2a\frac{ax+by+c}{a^{2}+b^{2}}$ and each $y$ with $y-2b\frac{ax+by+c}{a^{2}+b^{2}}$ (see here).

So, $r$ is $$d\left(x-2a\frac{ax+by+c}{a^{2}+b^{2}}\right)+e\left(y-2b\frac{ax+by+c}{a^{2}+b^{2}}\right)+f=0.$$

Or (doing a bit of algebra), $r$ is

$$\left[\left(b^{2}-a^{2}\right)d-2abe\right]x+\left[\left(a^{2}-b^{2}\right)e-2abd\right]y+f\left(a^{2}+b^{2}\right)-2c\left(ad+be\right)=0.$$